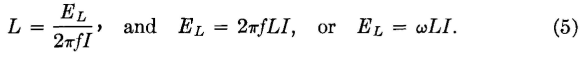Self-Inductance

Thus

where e₁ and i₁ are in the same circuit, and L is the coefficient of self-inductance.'' In this equation e₁ is the instantaneous induced electromotive force in volts, L is the self-inductance in henrys, and di₁/dt is the instantaneous rate of change of current in amperes per second.

The magnitude of the instantaneous induced electromotive force is e₁ = N dφ₁/10⁸dt. If this is substituted in equation 2, the magnitude of the self-inductance becomes

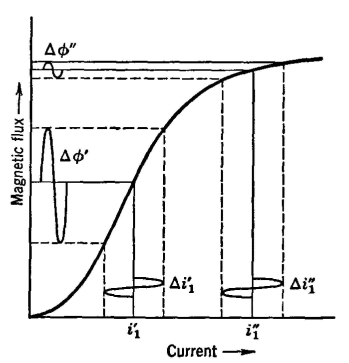
Communication equipment such as coils and transformers often have closed cores of ferromagnetic material. Also, coils sometimes have direct-current and alternating-current components flowing simultaneously in the windings. The inductance of such units can be found by equation 3, assuming that the magnetic characteristics of the material are known. This is shown by Fig. 1 which illustrates the way in which the magnetic flux φ varies in a ferromagnetic core with the current i₁ that produces it. Suppose that the value of the direct-current components is i₁' and that the alternating-current component is as shown by Δi₁'; then, the corresponding flux change will be Δφ'. Hence, dφ₁/di₁ of equation 3 will have a certain value, and the self-inductance L a certain magnitude. Now suppose that the value of the direct-current component i₁'' is different from i₁', being larger as shown in Fig. 1. The same change in current Δi₁" now produces but a very small change in magnetic flux Δφ", and hence dφ₁/di₁ of equation 3 will be very small and the inductance will be much less than when the direct-current component is at i₁'. Because of these variations, the inductance of a coil on a ferromagnetic core is called the incremental self-inductance, or merely incremental inductance. This may be regarded as a non-linear self-inductance.

Figure 1. Equal current changes Δi1' and Δi1'' do not produce the same flux changes Δφ' and Δφ'' if different values of direct current i1' and i1" flow through a coil with a closed core of iron or other ferromagnetic material. Thus, the incremental inductance depends on the value of the direct current component.

For coils and transformers with air cores, or ferromagnetic cores containing large air gaps, the inductance can be found by equation 3, or by the simplified form

In such equipment the inductance is essentially independent of the magnitude of the current. The flux φ₁ produced by current i₁ is found by the usual methods. The self-inductance L will be in henrys when N is the number of turns, φ₁ is in lines, and i₁ is the current in amperes. This may be regarded as a linear self-inductance.

Sometimes inductance is measured with ordinary alternating-current measuring instruments that indicate effective values. For steady-state sinusoidal conditions and effective values, equation 3 becomes

In these equations E_L is the magnitude of the effective value of the voltage drop in volts caused by the inductive reactance (excluding that caused by the effective resistance), I is the magnitude of the effective value of current in amperes, and f is the frequency in cycles per second. Such a determination would necessitate the use of a voltmeter, an ammeter, and a wattmeter to find the effective resistance or power-factor angle so that the reactive voltage drop E_L could be separated from the total voltage drop across the circuit or coil. The voltage E_L leads the current I by 90°. If the coil saturates and if the impressed voltage is sinusoidal, the current will be distorted and will contain harmonics. In this event, the ammeter will read the effective value of the current, and equation 5 will give effective self-inductance. A discussion of inductance when iron is present is given in reference 2,