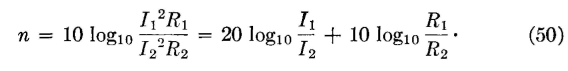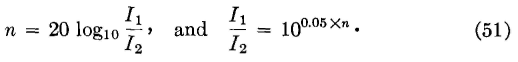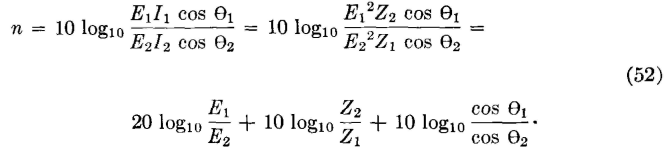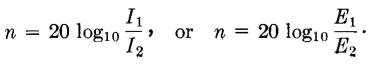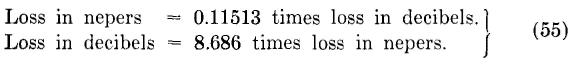The Decibel

The decibel is defined¹ as "one-tenth of a bel, the number of decibels denoting the ratio of two amounts of power being 10 times the logarithm to the base 10 of this ratio." The abbreviation db is used extensively. If P₁ and P₂ designate two amounts of power, and if n is the number of decibels denoting their ratio,

Power is seldom measured directly in communication circuits. It is usually determined indirectly from current measurements made with thermocouples, or from voltage measurements made with vacuum-tube voltmeters. Because of these indirect measurements of power, confusion has resulted in the use of the decibel, and the reasons will now be explained.

Figure 30. Circuit for illustrating the meaning of the term decibel.

It is desired to determine the power loss in decibels of the network of Fig. 30. This is to be done from the ratio of the input current I₁ and the output current I₂. Since power is I²R, equation 49 can be written

If R₁/R₂ = 1.0, then the last term equals zero, and under these special conditions, in which the resistance components of the input impedance equals the resistance component of the load impedance, the power ratio and the loss in decibels is

Similarly, if the power loss is to be determined from voltage readings, where E_l is the voltage impressed across the network and E₂ is the voltage across the load, since power = EI cosθ, equation 49 can be written

If it happens that Z₁ equals Z₂ in both magnitude and phase, then the last two terms become zero, and under these special conditions the power ratio and the loss in decibels is

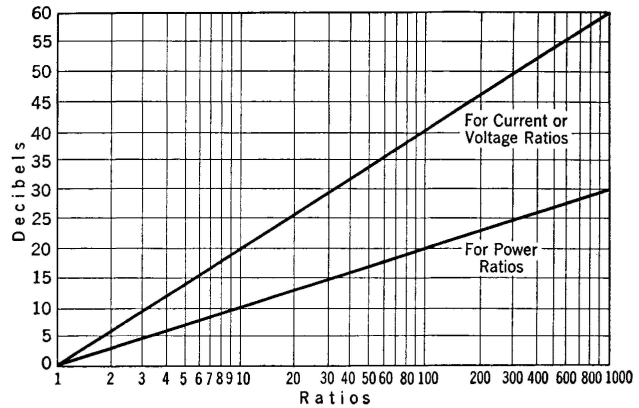
The confusion mentioned previously resulted from using equations 51 and 53 to determine power ratios in decibels in circuits that were not matched and did not meet the special conditions explained. Most telephone lines and apparatus are matched for maximum power transfer, and thus the impedance relations are such that equations 51 and 52 can be used without error. However, many circuits and much equipment are not matched for maximum power transfer, and hence these equations do not apply.

It is common practice to use equations 51 and 53 in circuits in which the impedances are not matched, but when so used these equations do not give power ratios in decibels but instead express current or voltage ratios in decibels. This is in accordance with the Standards,¹ but the usage should be accompanied by a statement of the specific application.

Gains in decibels as well as losses are expressed by equations 49, 51, and 53. In all instances the larger number is divided by the smaller, and the terminology "gain" or "loss" is used.

Equations 49, 51, and 53 can be plotted as in Fig. 31. With these curves, the gain or loss in decibels can be found. Also, gains or losses can be determined from Table V.

Figure 31. Curves for gain or loss in decibels, from current, voltage, or power ratios.

TABLE V

RELATIONS BETWEEN DECIBELS AND FRACTIONAL Loss OB GAIN IN POWER

Transmission losses are sometimes expressed in nepers. From equations 51 and 53, the loss in decibels is

If the natural or Napierian base for the logarithms is used,

where n' is the loss (or gain) in nepers. The relation between the natural and common logarithms is ln x = 2.3026 log₁₀ x. Therefore, from equation 54, n' = 2.3026 log₁₀ I₁/I₂. From equation 51, n/20 = log₁₀I₁/I₂, and