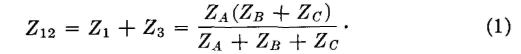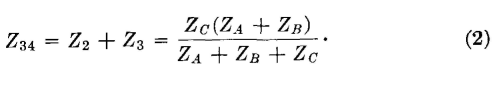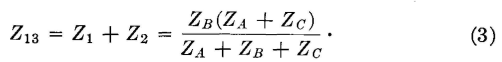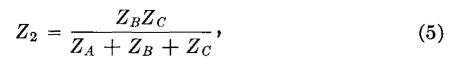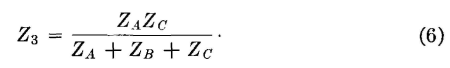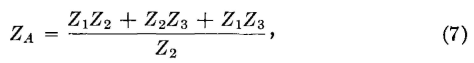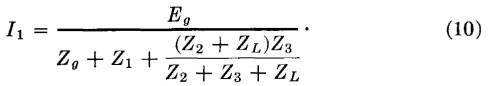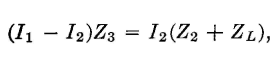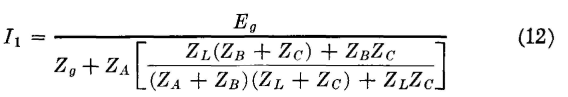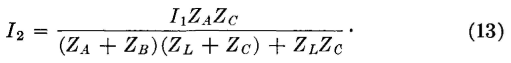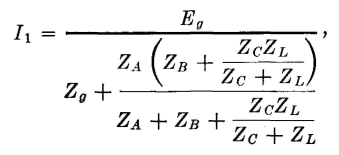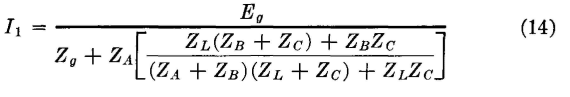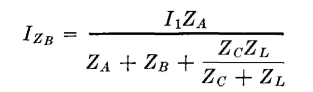Equivalence of T and Pi Sections

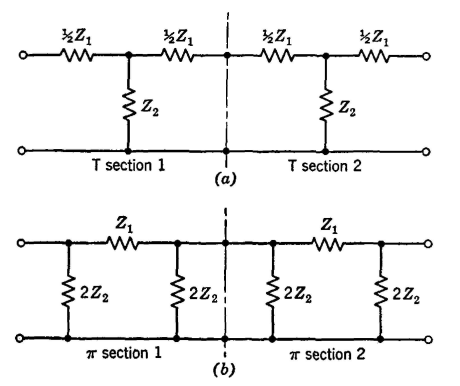
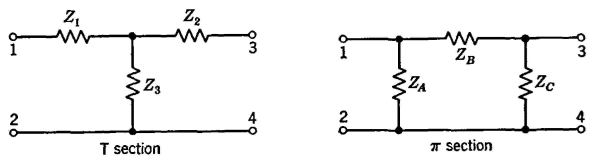
In communication circuits it sometimes is desired to find the π section that is equivalent to a T section, or vice versa. Two networks are of general equivalence¹ "if one network can replace another network in any system whatsoever without altering in any way the electrical operation of that portion of the system external to the network." Two networks are of limited equivalence¹ "if one network can replace another network only in some particular system without altering in any way the electrical operation of that portion of the system external to the networks." In the following discussion limited equivalence will be investigated. It is very important to note that networks often are constructed of impedances that vary with frequency; usually, networks are equivalent only at a given frequency.

Figure 5. The circuit of (a) is obtained by selecting the portion A-B of Fig. 4. The circuit of (6) is obtained by selecting the portion C-D of Fig. 4.

In Fig. 7 are shown T and π networks. To derive the transformation equations from which an equivalent π section can be designed if

Figure 6. T and π sections.

a T section is known (or vice versa) three equations will be written. For the T section, the impedance Z₁₂ measured between terminals

Figure 7. Circuits for deriving network transformation equations.

1-2 is Z₁₂ = Z₁ + Z₃, and for the π section the impedance Z₁₂ = Z_A(Z_B + Z_C)/(Z_A + Z_B + Z_C). When these are equated,

The corresponding equations for impedances measured between terminals 3-4 are

The corresponding equations for impedances measured between terminals 1-3 are

These three equations can be solved simultaneously for Z₁, Z₂, and Z₃ in terms of Z_A, Z_B, and Z_C. By adding equations 1 and 3, and subtracting equation 2, it is found that

Likewise, adding equations 2 and 3, and subtracting equation 1 gives

and adding equations 1 and 2, and subtracting equation 3 gives

These equations are for transformation from a π to a T network. To make transformations from T to a π network, the equations prove to be^2,3

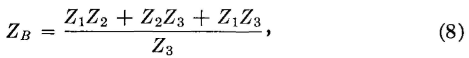
and

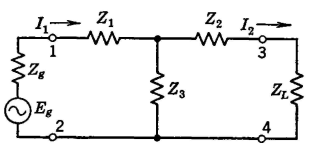
It is now desired to show that if the two networks are related according to these equations they are equivalent and can replace each other without altering the circuit operation. For this Fig. 8 will be used, in which the two circuits, related in accordance with the equations just given, are connected between identical sources of voltage E_g, and identical load impedances Z_L. If it can be shown that in each circuit the identical generators supply currents I₁ that are exactly the same and that the identical load impedances Z_L receive currents I₂ that are exactly the same, then the T and π sections are equivalent as far as terminals 1-2 and 3-4 are concerned.

For the T section of Fig. 8,

Because the voltage drops across two parallel branches must be equal,

and

Figure 8. Networks for studying conditions of limited equivalence.

The next step is to substitute in these two equations the values of Z₁, Z₂, and Z₃ given in equations 4, 5, and 6. Making these substitutions in equation 10 and simplifying the expression gives

Making these substitutions in equation 11 gives

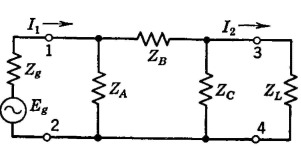
It now remains to derive expressions for I₁ and I₂ for the π section of Fig. 8, in terms of Z_A, Z_B, and Z_c and to ascertain if these expressions agree with equations 12 and 13. Thus, for the π section of Fig. 8,

and simplifying,

To find the current I₂ in the π section of Fig. 8 first it is necessary to find the current in impedance Z_B, which can be determined from the relation

and

Similarly,

Substituting the value of I_ZB in this expression gives

It has been shown that equations 12 and 13 derived for the T section are identical to equations 14 and 15 derived for the π section. This proves that the sections will perform exactly alike when inserted between a source of voltage and a load impedance and that so far as terminals 1-2 and 3-4 are concerned T and π networks related by equations 4, 5, and 6, or 7, 8, and 9 are equivalent.