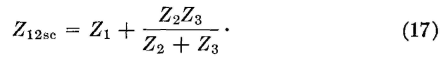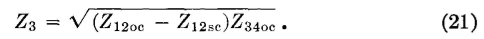| Electrical Communication is a free textbook on the basics of communication technology. See the editorial for more information.... |

|

Home  Electric Networks Electric Networks  Equivalent Networks Equivalent Networks |
|||






|
|||
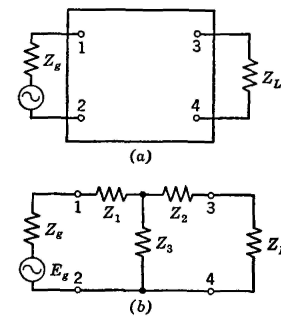
Equivalent NetworksIn the preceding section the value of each impedance of Fig. 9 (a) was known, and the reduction to the simple T network was made by transformation equations. Sometimes a circuit or device is in a "black box" (Fig. 10), the values of the impedances are unknown, and it is desired to determine the simple equivalent T or π network. For limited equivalence between the two sets of input terminals 1-2 and the two sets of output terminals 3-4, the input currents I1 to the two networks must be identical and the output currents I2 to the loads ZL must be identical (in both magnitude and phase). Of course, this also implies that the voltage across terminals 1-2 must be identical, and the output voltages across terminals 3-4 must be identical when the networks are connected between the same generator and the same load impedance ZL. An investigation will show that if the input current I1 does not equal the output current I2, there must be a shunt element such as Z3 in an equivalent network (Fig. 9 or 10). Similarly, if the input voltage E12 does not equal the output voltage E34, there must be series elements such as Z1 and Z2. Thus, three impedances are required in an equivalent network. These three impedances may be in a T configuration as in Fig. 10, or may be transformed into a π configuration.
The individual elements within the black box of Fig. 10 in general cannot be determined. It is known, however, that, at a given frequency, some T network will be equivalent. The values of Z1, Z2, and Z3 of this equivalent T network must be determined from measurements on the unknown network. Thus, if the input impedance between terminals 1-2 is measured with the output terminals 3-4 open circuited and if this is called Z12oc, then
If the input impedance Z12sc is measured between input terminals 1-2 with the output terminals 3-4 short circuited, then
If the output impedance Z34oc is measured between output terminals 3-4 with the input terminals 1-2 open circuited, then
From these three equations,
and
Equation 21 is found by substituting equations 19 and 20 in equation 17 and solving for Z3.
|
|||
Home  Electric Networks Electric Networks  Equivalent Networks Equivalent Networks |
|||
Last Update: 2011-05-30