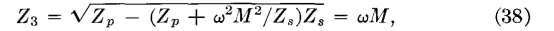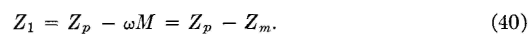| Electrical Communication is a free textbook on the basics of communication technology. See the editorial for more information.... |

|

Home  Electric Networks Electric Networks  Transformer Equivalent Networks Transformer Equivalent Networks |
|||||






|
|||||
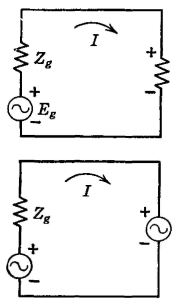
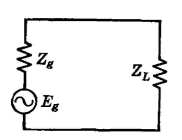
Transformer Equivalent NetworksFor the purposes of circuit analysis, it is sometimes desired to replace a transformer by an equivalent T (or π) network. The equivalent T network for a transformer can be found from three impedance measurements and the use of equations 19, 20, and 21. From Fig. 17 it is seen that Z12oc = Zp, the impedance of the primary of the transformer; also, that Z34oc = Zs, the impedance of the secondary. The impedance of the primary, with the secondary short circuited is, from coupled-circuit theory (page 67) ?
Z12sc = Zp + (ωM)2/Zs. Thus, it is possible from these three measurements to determine both the important constants of a transformer, and the equivalent T network. If the values just discussed are inserted in equations 21, 20, and 19 in the order given,
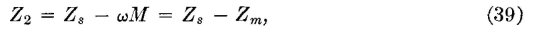
and
The reason that ωM = Zm, where Zm is called the mutual impedance, can be explained in the following manner. From Fig. 17, when the secondary is open, the voltage E34 across the secondary is equal to the IpZ3 voltage drop. Thus, Z3 = E34/Ip = ωMIp/Ip = ωM = Zm, the term mutual impedance being used because, for the actual transformer of Fig. 17, the secondary voltage #34 is being divided by the primary current IP. Transformers are used in communication circuits for impedance matching (page 68). For such purposes, an ideal transformer is assumed. Such a transformer will change the magnitude of the load impedance without altering the angle of the load impedance and introduces no losses into the circuit. An ideal transformer is assumed in making possible maximum power transfer under the conditions of the second maximum power transfer theorem.
|
|||||
Home  Electric Networks Electric Networks  Transformer Equivalent Networks Transformer Equivalent Networks |
|||||
Last Update: 2011-06-05