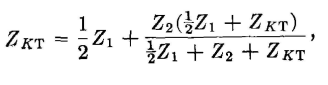Iterative Impedance

Figure 19. Circuits for deriving the equations for midseries and midshunt iterative impedances.

The iterative impedance at a pair of terminals such as 1-2 or 3-4 of Fig. 19 is defined¹ as "the impedance which will terminate the other pair of terminals in such a way that the impedance measured at the first pair of terminals is equal to this terminating impedance." For an unsymmetrical section the iterative impedances at the two sets of terminals are different; for a symmetrical section the iterative impedances are equal and the same as the image impedances.¹ Because of their wide use, symmetrical sections will be treated in the remainder of this section.

The notation used for the elements of the T and π sections of Fig. 19 are the same as was used for the sections of Fig. 6. This notation is usually employed for the circuits now to be considered.

The input impedances at terminals 1-2 of Fig. 19 (a) when terminals 3-4 are terminated in the iterative impedance Z_KT of the T network is

which, when solved for Z_KT, gives

For the π section, the iterative impedance Z_Kπ is the input impedance at terminals 1-2 of Fig. 19(b) when terminals 3-4 are terminated in the iterative impedance Z_Kπ of the π network. Thus

The iterative impedance of a network such as shown in Fig. 19 (a) or (b) is readily determined from open-circuit and short-circuit impedance measurements. Thus, if an impedance bridge is used to measure the input impedance at terminals 1-2 of the T section of Fig. 19 (a) when terminals 3-4 are open,

and the input impedance at terminals 1-2 with terminals 3-4 short circuited is

If these two equations are multiplied together and the square root taken,

Although this derivation was for a T section, it can be shown that the iterative impedance of a π section also can be found from open-circuit and short-circuited measurements.