| The ebook Elementary Calculus is based on material originally written by H.J. Keisler. For more information please read the copyright pages. |

|

Home  Real and Hyperreal Numbers Real and Hyperreal Numbers  The Real Line The Real Line  The Real Line The Real Line |
|






|
|
The Real Line
Familiarity with the real number system is a prerequisite for this course. A review of the rules of algebra for the real numbers is given in the appendix. For convenience, these rules are also listed in a table inside the front cover. The letter R is used for the set of all real numbers. We think of the real numbers as arranged along a straight line with the integers (whole numbers) marked off at equal intervals, as shown in Figure 1.1.1. This line is called the real line.
Figure 1.1.1 The real line. In grade school and high school mathematics, the real number system is constructed gradually in several stages. Beginning with the positive integers, the systems of integers, rational numbers, and finally real numbers are built up. One way to construct the set of real numbers is as the set of all nonterminating decimals. After constructing the real numbers, it is possible to prove the familiar rules for sums, differences, products, quotients, exponents, roots, and order. In this course, we take it for granted that these rules are familiar to the student, so that we can proceed as quickly as possible to the calculus. Before going on, we pause to recall two special points that are important in the calculus. First, division by zero is never allowed. Expressions such as
are always considered to be undefined. Second, a positive real number c always has two square roots, On the other hand, every real number has one real cube root. If c > 0, c has the positive cube root In calculus, we often deal with sets of real numbers. By a set S of real numbers, we mean any collection of real numbers, called members of S, elements of S, or points in S.
|
|
Home  Real and Hyperreal Numbers Real and Hyperreal Numbers  The Real Line The Real Line  The Real Line The Real Line |
|
Last Update: 2006-11-05


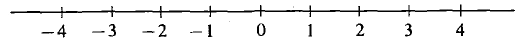
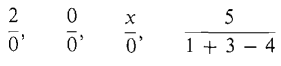
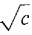 and -
and -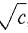 , and
, and 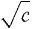 always stands for the positive square root. Negative real numbers do not have real square roots. For each positive real number c,
always stands for the positive square root. Negative real numbers do not have real square roots. For each positive real number c, 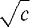 is positive and
is positive and 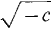 is undefined.
is undefined.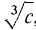 and -c has the negative cube root
and -c has the negative cube root