Real Function of One Variable

The next two sections are about real numbers only. The calculus deals with problems in which one quantity depends on one or more others. For example, the area of a circle depends on its radius. The length of a day depends on both the latitude and the date. The price of an object depends on the supply and the demand. The way in which one quantity depends on one or more others can be described mathematically by a function of one or more variables.

Thus f(a) = b means that the ordered pair (a, b) is an element of f.

Here is one way to visualize a function. Imagine a black box labeled f as in Figure 1.2.1. Inside the box there is some apparatus, which we can't see. On both the left and right sides of the box there is a copy of the real line, called the input line and output line, respectively. Whenever we point to a number a on the input line, either one point b will light up on the output line to tell us that f(a) = b, or else nothing will happen, in which case f(a) is undefined.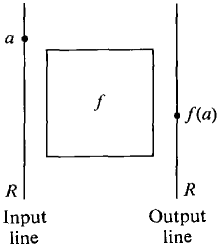

Figure 1.2.1