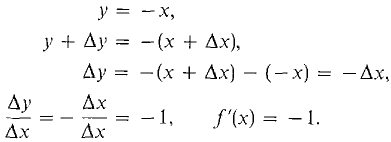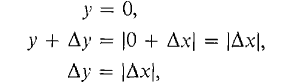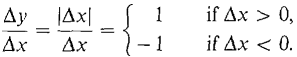| The ebook Elementary Calculus is based on material originally written by H.J. Keisler. For more information please read the copyright pages. |

|

Home  Differentiation Differentiation  Derivatives Derivatives  Examples Examples  Example 4: Absolute Value Function Example 4: Absolute Value Function |
||||||||






|
||||||||
Example 4: Absolute Value Function
Case 1 Find the derivative of f(x) = |x|. x > 0. In this case |x| = x, and we have
Case 2 x < 0. Now |x| = - x, and
Case 3 x = 0. Then
and
The standard part of Δy/Δx is then 1 for some values of Δx and -1 for others. Therefore f'(x) does not exist when x = 0. In summary,
Figure 2.1.6 shows f(x) and f'(x).
Figure 2.1.6 The derivative has a variety of applications to the physical, life, and social sciences. It may come up in one of the following contexts.
|
||||||||
Home  Differentiation Differentiation  Derivatives Derivatives  Examples Examples  Example 4: Absolute Value Function Example 4: Absolute Value Function |
||||||||
Last Update: 2006-11-15