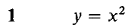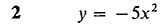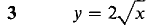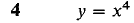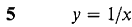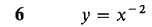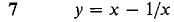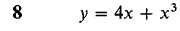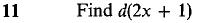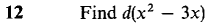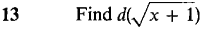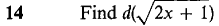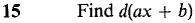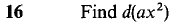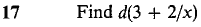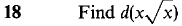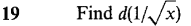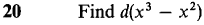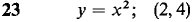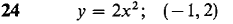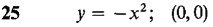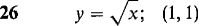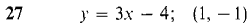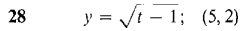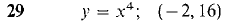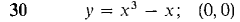Problems

In Problems 1-8, express Δy and dy as functions of x and Δx, and for Δx infinitesimal find an infinitesimal s such that Δy = dy + ε Δx.

9           If y = 2x² and z = x³, find Δy, Δz, dy, and dz.

10           If y = 1/(x + 1) and z = 1/(x + 2), find Δy, Δz, dy, and dz.

21            Let y = √x, z = 3x. Find d(y + z) and d(y/z).

22            Let y = x^-1 and z = x³. Find d(y + z) and d(yz).

In Problems 23-30 below, find the equation of the line tangent to the given curve at the given point.

31             Find the equation of the line tangent to the parabola y = x² at the point (x₀, x^₀2,).

32            Find all points P(x₀, x₀²,) on the parabola y = x² such that the tangent line at P passes through the point (0, -4).

33            Prove that the line tangent to the parabola y = x² at P(x₀, x₀²) does not meet the parabola at any point except P.