| The ebook Elementary Calculus is based on material originally written by H.J. Keisler. For more information please read the copyright pages. |

|

Home  Differentiation Differentiation  Inverse Functions Inverse Functions  Inverse Function Rule Inverse Function Rule |
|






|
|
Inverse Function Rule
The following rule shows that the derivatives of inverse functions are always reciprocals of each other. INVERSE FUNCTION RULE Suppose f and g are inverse functions, so that the two equations y=f(x) and x = g(y) have the same graphs. If both derivatives f'(x) and g'(y) exist and are nonzero, then
that is,
PROOF Let Δx be a nonzero infinitesimal and let Δy be the corresponding change in y. Then Δy is also infinitesimal because f'(x) exists and is nonzero because f(x) has an inverse function. By the rules for standard parts,
Therefore
The formula
in the Inverse Function Rule is not as trivial as it looks. A more complete statement is
Sometimes it is easier to compute dx/dy than dy/dx, and in such cases the Inverse Function Rule is a useful method.
|
|
Home  Differentiation Differentiation  Inverse Functions Inverse Functions  Inverse Function Rule Inverse Function Rule |
|
Last Update: 2010-11-25


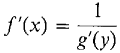
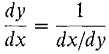
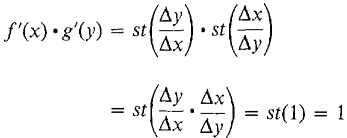
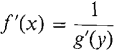
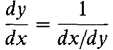
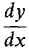 computed with x the independent variable
computed with x the independent variable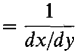 computed with y the independent variable.
computed with y the independent variable.