The ebook Elementary Calculus is based on material originally written by H.J. Keisler. For more information please read the copyright pages.

Home Continuous Functions Limits Theorem 2: One-sided Limits
 
del.icio.us Reddit Facebook StumbleUpon MySpace Twitter Search the VIAS Library  |  Index

Theorem 2: One-sided Limits

Example 7
Example 8
Example 9

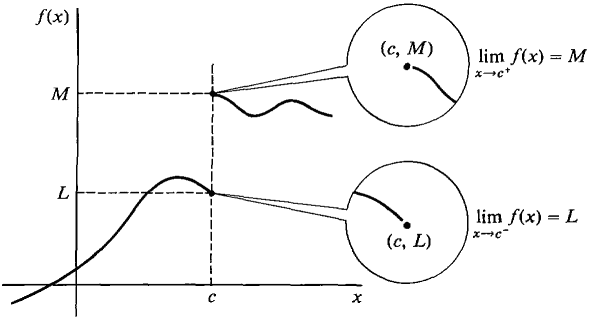
In the above examples the function behaves differently on one side of the point 0 than it does on the other side. For such functions, one-sided limits are useful.

We say that

limx→c+ f(x) = L

if whenever x > c and x ≈ c, f(x) ≈ L.

limx→c- f(x) = L

means that whenever x < c and x ≈ c, f(x) ≈ L. These two kinds of limits, shown in Figure 3.3.4, are called the limit from the right and the limit from the left.

03_continuous_functions-69.gif

Figure 3.3.4 One-sided limits.

THEOREM 2

A limit has value L,

lim f(c) = L,

if and only if both one-sided limits exist and are equal to L,

limx→c- f(x) = limx→c+ f(x) = L.

PROOF

If limx→c f(x) = L, it follows at once from the definition that both one-sided limits are L.

Assume that both one-sided limits are equal to L. Let x ≈ c, but x ≠ c. Then either x < c or x > c. If x < c, then because limx→c- f(x) = L, we have f(x) ≈ L. On the other hand if x > c, then limx→c+ f(x) = L gives f(x) ≈ L. Thus in either case f(x) ≈ L. This shows that limx→c f(x) = L.

When a limit does not exist, it is possible that neither one-sided limit exists, that just one of them exists, or that both one-sided limits exist but have different values.

Example 7 Continued
Example 8 Continued
Example 9 Continued

Home Continuous Functions Limits Theorem 2: One-sided Limits

Last Update: 2006-11-05