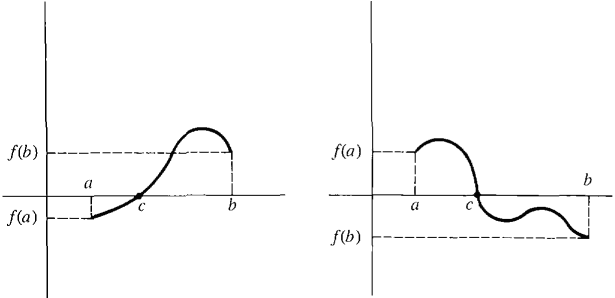| The ebook Elementary Calculus is based on material originally written by H.J. Keisler. For more information please read the copyright pages. |
|
Home  Continuous Functions Properties of Continuous Functions Intermediate Value Theorem |
|
 Search the VIAS Library | Index
|
  |
Intermediate Value Theorem
INTERMEDIATE VALUE THEOREM Suppose the real function f is continuous on the closed interval [a, b] and f(x) is positive at one endpoint and negative at the other endpoint. Then f has a zero in the interval (a, b); that is, f(c) = 0 for some real c in (a, b). Discussion There are two cases illustrated in Figure 3.8.6: f(a) < 0 < f(b) and f(a) > 0 > f(b).
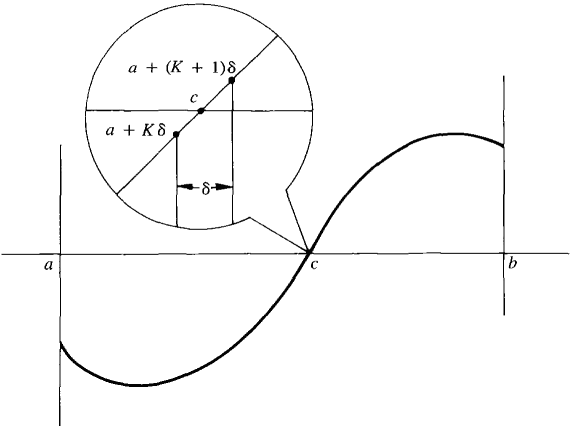
Figure 3.8.6 In the first case, the theorem says that if a continuous curve is below the x-axis at a and above it at b, then the curve must intersect the x-axis at some point c between a and b. Theorem 3 in the preceding Section 3.7 on curve sketching is simply a reformulation of the Intermediate Value Theorem. SKETCH OF PROOF We assume f(a) < 0 < f(b). Let H be a positive infinite hyperinteger and partition the interval [a, b]* into H equal parts a, a + δ, a + 2δ,..., a + Hδ = b. Let a + Kδ be the last partition point at which f(a + Kδ) < 0. Thus f(a + Kδ) < 0 ≤ f(a + (K+ 1)δ). Since f is continuous, f(a + Kδ) is infinitely close to f(a + (K + 1)δ). We conclude that f(a + Kδ) ≈ 0 (Figure 3.8.7). We take c to be the standard part of a + Kδ, so that f(c) = st(f(a + Kδ)) = 0.
|
|
| Home Continuous Functions Properties of Continuous Functions Intermediate Value Theorem |
|
Last Update: 2006-11-05