Antiderivative of Velocity

If a particle moves along the y-axis with continuous velocity v = f(t), the position y = F(t) is an antiderivative of the velocity, because v = dy/dt. The Fundamental Theorem of Calculus shows that the distance moved (the change in y) between times t=a and t=b is equal to the definite integral of the velocity,

distance moved = F(b) - F(a) =

A particle moves along the y-axis with velocity v = 8t³ cm/sec. How far does it move between times f = -1 and t = 2 sec? The function G(t) = 2t⁴ is an antiderivative of the velocity v = 8t³. Thus the definite integral is

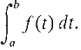
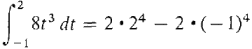distance moved == 30 cm.