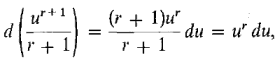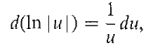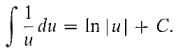| The ebook Elementary Calculus is based on material originally written by H.J. Keisler. For more information please read the copyright pages. |

|

Home  Integral Integral  Indefinite Integrals Indefinite Integrals  Integration Rules Integration Rules |
|||||||||||||||||||||||||||||||||
| See also: Integral of Products | |||||||||||||||||||||||||||||||||






|
|||||||||||||||||||||||||||||||||
Integration Rules
THEOREM 2 Let u and v be functions of x whose domains are an open interval I and suppose du and dv exist for every x in I.
Discussion The Power Rule gives the integral of ur when r Constant Rule
Sum Rule
In the Constant and Sum Rules we are multiplying a family of functions by a constant and adding two families of functions. If we do either of these two things to families of functions differing only by a constant, we get another family of functions differing only by a constant. For example, 7(3x4 + C) = 21x4 + 7C = 21x4 + C' is the family of all functions equal to 21x4 plus a constant. Similarly, (3√x + C) + (5x - √x + D) = 5x + 2√x + (C + D) = 5x + 2√x + C is the family of all functions equal to 5x + 2√x plus a constant. PROOF OF THEOREM 2
Rules (v)-(viii) are similar. Only the last formula, (viii), requires an explanation. The absolute value in ln |u| comes about by combining the two cases u > 0 and u < 0. When u > 0, u = |u| and d(ln |u|) = d(ln u) = -du. When w < 0, ln u is undefined, but |u| = - u and ln |u| = ln (-u). Thus d(ln|u|) = d(ln(-u)) = -1/u d(-u) = -1/u du. Thus, in both cases, when u
|
|||||||||||||||||||||||||||||||||
Home  Integral Integral  Indefinite Integrals Indefinite Integrals  Integration Rules Integration Rules |
|||||||||||||||||||||||||||||||||
Last Update: 2006-12-01


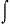 du = u + C.
du = u + C.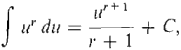 where r is rational, r
where r is rational, r 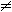 -1,and u > 0 on I.
-1,and u > 0 on I.