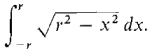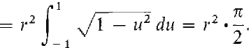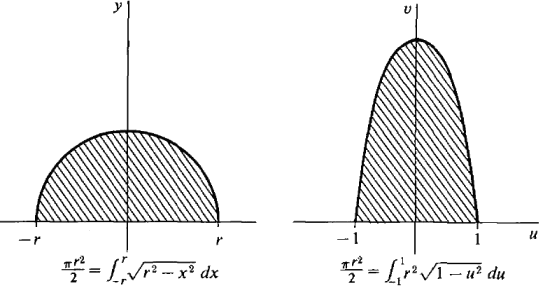Area of a Semicircle

Example 7: Area Under A Semicircle

We can use integration by change of variables to derive the formula for the area of a circle, A = r²π, where r is the radius. It is easier to work with a semicircle because the semicircle of radius r is just the region under the curve

r ≤ x ≤ r.

To start with we need to give a rigorous definition of π. By definition, π is the area of a unit circle. Thus π is twice the area of the unit semicircle, which means:

To evaluate this integral we let x = ru. Then dx = r du. When x = ±r,u = ±1. Thus

Therefore the semicircle has area r²π/2 and the circle area r²π (Figure 4.4.6).

Figure 4.4.6