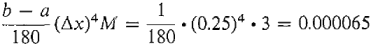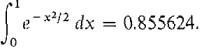Example 3: Simpsons Rule Applied

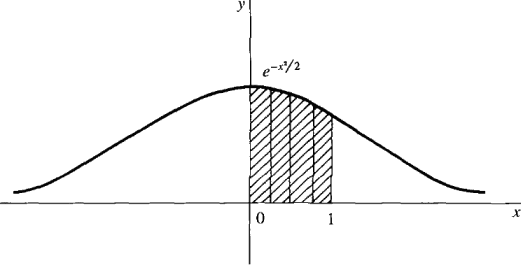
Use Simpson's Rule with Δx = 0.25 to approximate the integral

and find the error estimate.

The curve is the normal (bell-shaped) curve used in statistics, shown in Figure 4.6.5. We are to divide the interval [0, 1] into four subintervals of equal length Δx = 0.25. The following table shows the values of x and y and the coefficient to be used in Simpson's approximation for each partition point.

Figure 4.6.5 Example 3

The sum used in the Simpson approximation is then

[1.000000 + 4 · (0.969233) + 2 · (0.882496) + 4 · (0.754840) + 0.606531] = 10.267816

To get the Simpson approximation, we multiply this sum by Δx/3:

S = (10.267816) · (0.25)/3 = 0.855651.

To find the error estimate we need the fourth derivative of

y = e^-x²/2.

The fourth derivative can be computed as usual and turns out to be

y⁽⁴⁾ = (x⁴ - 6x² + 3)e^-x²/2.

On the interval [0, 1], y⁽⁴⁾ is decreasing because both x⁴ - 6x² + 3 and - x²/2 are decreasing, and therefore y⁽⁴⁾ has its maximum value at x = 0 and its minimum value at x = 1,

maximum: y⁽⁴⁾(0) = 3

minimum: y⁽⁴⁾(1) = -1.213061

The maximum value of the absolute value |y⁽⁴⁾| is thus M = 3. The error estimate in Simpson's Rule is then

This shows that the integral is within 0.000065 of the approximation; that is,

or using inequalities,

For comparison, a more accurate computation with a smaller Δx shows that the actual value to six places is

The Trapezoidal Rule for this integral and the same value of Δx = 0.25 give an approximate value of 0.85246 for the integral and an error estimate of 0.00521.