The ebook Elementary Calculus is based on material originally written by H.J. Keisler. For more information please read the copyright pages.

Home Limits, Analytic Geometry, and Approximations Parabolas Graphing a Parabola
 
del.icio.us Reddit Facebook StumbleUpon MySpace Twitter Search the VIAS Library  |  Index

Graphing a Parabola

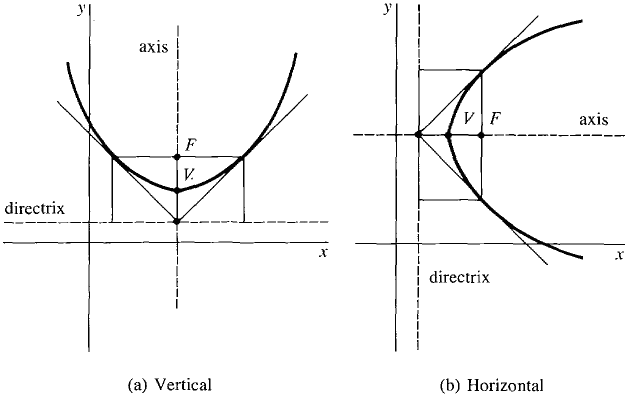
GRAPHING A PARABOLA y = ax2 + bx + c

Step 1 Make a table of values of x, y, dy/dx, and d2y/dx2 at x → -∞, x = -b/2a (the vertex), and x → ∞.
Step 2 Compute the axis, vertex, focus, and directrix, and draw them.
Step 3 Draw the two squares with sides along the axis and directrix and a corner at the focus. The two new corners level with the focus, P and Q, are on the parabola because they are equidistant from the focus and the directrix.
Step 4 Draw the diagonals of the squares through P and Q. These are the tangent lines to the parabola at P and Q. (The proof of this fact is left as a problem.)
Step 5 Draw the parabola through the vertex, P, and Q, using the table and tangent lines. The parabola should be symmetrical about the axis x = -b/2a. See Figure 5.4.8(a).

A horizontal parabola x = ay2 + by + c can be graphed by the same method with the roles of x and y interchanged, as in Figure 5.4.8(b).

05_limits_g_approx-267.gif

Figure 5.4.8

Example 2 (Continued): Sketching a Parabola
Example 3 (Continued) Sketching a Parabola

Home Limits, Analytic Geometry, and Approximations Parabolas Graphing a Parabola

Last Update: 2006-11-05