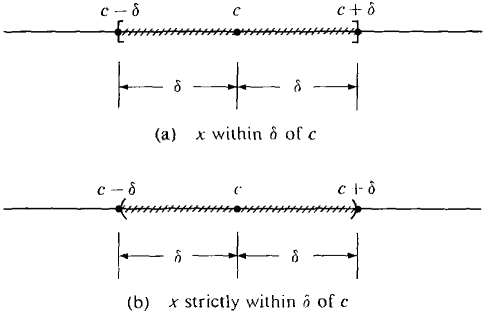The ε, δ Condition for Limits

The traditional calculus course is developed entirely without infinitesimals. The starting point is the concept of a limit. The intuitive idea of lim_x→c f(x) = L is: For every real number x which is close to but not equal to c, f(x) is close to L.

It is hard to make this idea into a rigorous definition, because one must clarify the word "close". Indeed, the whole point of our infinitesimal approach to calculus is that it is easier to define and explain limits using infinitesimals. The definition of limits in terms of real numbers is traditionally expressed using the Greek letters ε (epsilon) and δ (delta), and is therefore called the ε, δ condition for limits.

The ε, δ condition will be based on the notion of distance between two real numbers.

Notice that the distance |x - c| is just the difference between the larger and the smaller of the two numbers x and c. This is a place where the absolute value sign is especially convenient. The following simple but helpful lemma is illustrated in Figure 5.8.1.

Figure 5.8.1