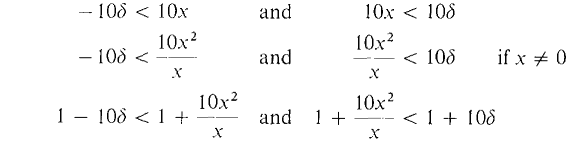Example 1

Consider the limit

When x = 0, the function f(x) = 1 + 10x²/x is undefined. When x is a real number close to but not equal to 0, f(x) is close to 1.

Now let us be more explicit. How should we choose x to get f(x) strictly within 1/5 of 1? To solve this problem we assume x is strictly within some distance δ of 0 and get inequalities for f(x).

By the lemma, we must find a δ > 0 such that whenever

- δ < x < δ and x ≠ 0,

we have 

1 - 1/5 < f(x) < 1 + 1/5.

Assume

Then

1 - 10δ < f(x) < 1 + 10δ.

If we set

δ = 1/50 ,

then

1 - 1/5 < f(x) < 1 + 1/5

This shows that

whenever

-1/50 < x < 1/50 and x ≠ 0, 1 - 1/5 < f(x) < 1 + 1/5.

In other words, whenever

0 < |x| < 1/50, | f(x) - 1| < 1/5.

A similar computation shows that for each ε > 0, if 0 < |x| < ε/10 then |f(x) - 1| < ε. Thus the ε, δ condition for lim_x→0 (1 + 10x²/x) = 1 is true, and, for a given ε, a corresponding δ is δ = ε/10.