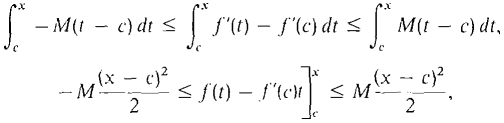Approximating Derivatives

In Section 3.3 we found that the derivative of f is given by the limit

If y = f(x),

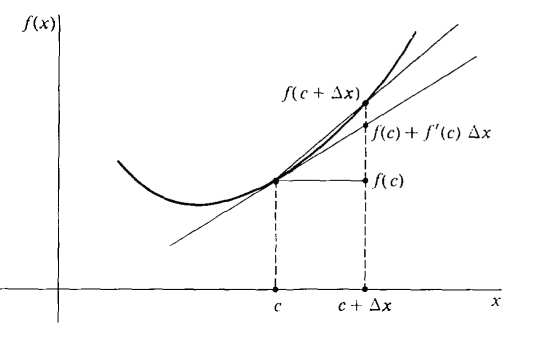
By definition this means that when the hyperreal number Δx is infinitely close to but not equal to zero, Δy/Δx is infinitely close to dy/dx.

By contrast, the for this limit says intuitively that when the real number Δx is close to but not equal to zero, Δy/Δx is close to dy/dx.

The ε, δ condition for the derivative can be given a geometric interpretation, shown in Figure 5.10.1. Consider the curve y = f(x), and suppose f'(c) exists. Draw the line tangent to the curve at c.

Figure 5.10.1

For Δx ≠ 0, draw the secant line which intersects the curve at the points (c, f(c)) and (c + Δx, f(c + Δx)). Then the tangent line will have slope f'(c) while the secant line will have slope

The ε, δ condition shows that if we take values of Δx closer and closer to zero, then the slopes of the secant line will get closer and closer to the slope of the tangent line.

Example 1

The ε, δ condition for the derivative is of theoretical importance but does not give an error estimate for the limit. When the function f has a continuous second derivative, we can get a useful error estimate in a different way. It is more convenient to work with one-sided limits.

By an error estimate for a limit

lim_x→0+ g(Δx) = L

we mean a real function E(Δx), 0 < Δx ≤ b, such that the approximation g(Δx) is always within E(Δx) of the limit L. In symbols,

|g(Δx) - L| ≤ E(Δx) for 0 < Δx ≤ b.

There is a similar theorem for the left-sided limit

with the error estimate ½M |Δx|.

Figure 5.10.2

Example 1 (Concluded)