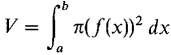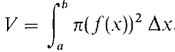Disc Method

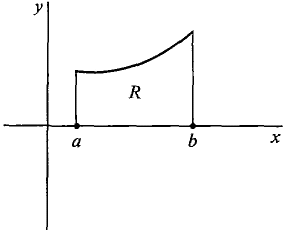
DISC METHOD: For rotations about the axis of the independent variable.

Let us first consider the region under a curve. Let R be the region under a curve y = f(x) from x = a to x = b, shown in Figure 6.2.3(a).

Figure 6.2.3 (a)	Figure 6.2.3 (b)

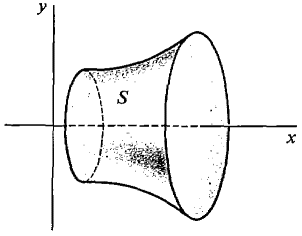
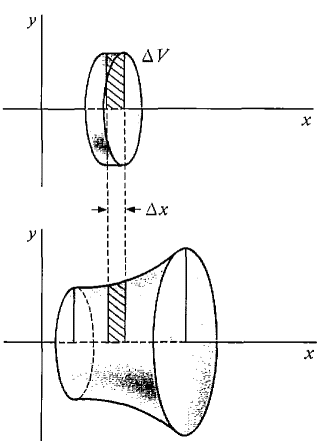
x is the independent variable in this case. To keep R in the first quadrant we assume 0 ≤ a < b and 0 ≤ f(x). Rotate R about the x-axis, generating the solid of revolution S shown in Figure 6.2.3(b). This volume is given by the formula below.

VOLUME BY DISC METHOD

To justify this formula we slice the region R into vertical strips of infinitesimal width Δx. This slices the solid S into discs of infinitesimal thickness Δx. Each disc is almost a cylinder of height Δx whose base is a circle of radius f(x) (Figure 6.2.4). Therefore

ΔV = π(f(x))² Δx (compared to Δx).

Then by the Infinite Sum Theorem we get the desired formula

Figure 6.2.4 Disc Method

Example 1: Right Circular Cone