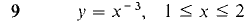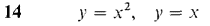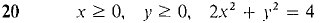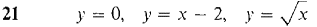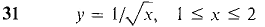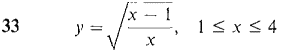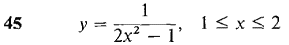Problems

In Problems 1-10 the region under the given curve is rotated about (a) the x-axis, (b) the y-axis. Sketch the region and find the volumes of the two solids of revolution.

In Problems 11-22 the region bounded by the given curves is rotated about (a) the x-axis, (b) the y-axis. Sketch the region and find the volumes of the two solids of revolution.

In Problems 23-34 the region under the given curve is rotated about the x-axis. Find the volume of the solid of revolution.

In Problems 35-46 the region is rotated about the x-axis. Find the volume of the solid of revolution.

47            A hole of radius a is bored through the center of a sphere of radius r (a < r). Find the volume of the remaining part of the sphere.

48            A sphere of radius r is cut by a horizontal plane at a distance c above the center of the sphere. Find the volume of the part of the sphere above the plane (c < r).

49            A hole of radius a is bored along the axis of a cone of height h and base of radius r. Find the remaining volume (a < r).

50            Find the volume of the solid generated by rotating an ellipse a² x² + b² y² = 1 about the x-axis. Hint: The portion of the ellipse in the first quadrant will generate half the volume.

51             The sector of a circle shown in the figure is rotated about (a) the x-axis, (b) the y-axis. Find the volumes of the solids of revolution.

52            The region bounded by the curves y = x², y = x is rotated about (a) the line y = -1, (b) the line x = -2. Find the volumes of the solids of revolution.

53            Find the volume of the torus (donut) generated by rotating the circle of radius r with center at (c, 0) around the y-axis (r < c).

54          (a) Find a general formula for the volume of the solid of revolution generated by rotating

the region bounded by the curves y = f(x), y = g(x), a ≤ x ≤ b, about the line y=-k. (b) Do the same for a rotation about the line x = -h.