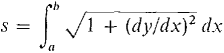| The ebook Elementary Calculus is based on material originally written by H.J. Keisler. For more information please read the copyright pages. |

|

Home  Applications of the Integral Applications of the Integral  Length of a Curve Length of a Curve  Parametric Curves Parametric Curves |
|||||






|
|||||
Parametric Curves
A natural example is the path of a moving particle where f is time. We give a formula for the length of such a curve. DEFINITION Suppose the functions x = f(t), y = g(t) have continuous derivatives and the parametric curve does not retrace its path for t in [a, b] The length of the curve is defined by
JUSTIFICATION
Figure 6.3.4 The infinitesimal piece of the curve (Figure 6.3.4) from t to t + Δt is almost a straight line, so its length Δs is given by
By the Infinite Sum Theorem,
The general formula for the length of a parametric curve reduces to our first formula when the curve is given by a simple equation x = g(y) or y = f(x). If y = f(x), a ≤ x ≤ b, we take x = t and get
If x = g(y), a ≤ y ≤ b, we take y = t and get
The following example shows what happens when a parametric curve does retrace its path.
|
|||||
Home  Applications of the Integral Applications of the Integral  Length of a Curve Length of a Curve  Parametric Curves Parametric Curves |
|||||
Last Update: 2010-11-25


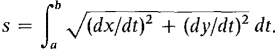
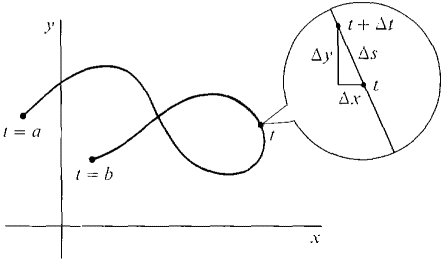
 (compared to Δt),
(compared to Δt),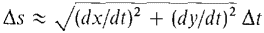 (compared to Δt).
(compared to Δt).