| The ebook Elementary Calculus is based on material originally written by H.J. Keisler. For more information please read the copyright pages. |

|

Home  Applications of the Integral Applications of the Integral  Area of a Surface of Revolution Area of a Surface of Revolution  Examples Examples  Example 1: Line Segment Example 1: Line Segment |
|






|
|
Example 1: Line Segment
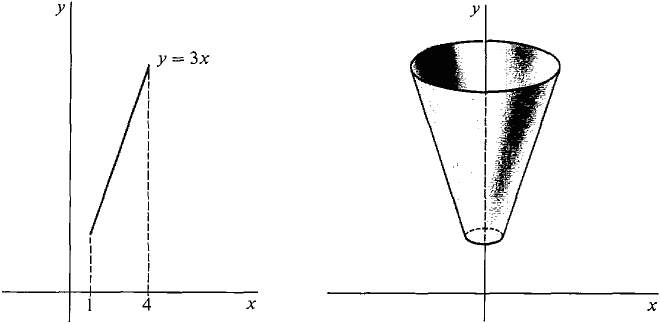
The line segment y = 3x, from x = 1 to x = 4, is rotated about the y-axis (Figure 6.4.7). Find the area of the surface of revolution. FIRST SOLUTION We use the integration formula, dy/dx = 3, so
Figure 6.4.7 SECOND SOLUTION This surface of revolution is a frustum of a cone, so the formula for the lateral area of a frustum can be used directly. From the diagram we see that the radii and slant height are: r1 = 1, r2 = 4, l = distance from (1,3) to (4, 12)
Then A = π(r1 + r2)l = π(1 + 4)3
|
|
Home  Applications of the Integral Applications of the Integral  Area of a Surface of Revolution Area of a Surface of Revolution  Examples Examples  Example 1: Line Segment Example 1: Line Segment |
|
Last Update: 2006-11-22


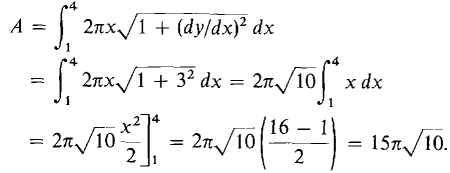
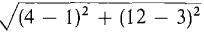
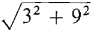
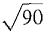
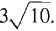
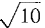 = 15π
= 15π