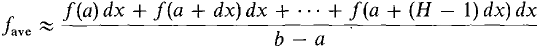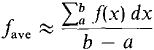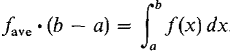| The ebook Elementary Calculus is based on material originally written by H.J. Keisler. For more information please read the copyright pages. |

|

Home  Applications of the Integral Applications of the Integral  Averages Averages  Average Value Average Value |
|||






|
|||
Average Value
Given n numbers yl, ..., yn, their average value is defined as
If all the yi are replaced by the average value yave, the sum will be unchanged, y1 + ... + yn = yave + ... + yave = nyave. If f is a continuous function on a closed interval [a, b], what is meant by the average value of f between a and b (Figure 6.5.1)?
Figure 6.5.1 Let us try to imitate the procedure for finding the average of n numbers. Take an infinite hyperreal number H and divide the interval [a, b] into infinitesimal subintervals of length dx = (b - a)/H. Let us "sample" the value of f at the H points a, a + dx, a + 2 dx, ..., a + (H - 1) dx. Then the average value of f should be infinitely close to the sum of the values of f at a, a + dx, ..., a + (H - 1) dx, divided by H. Thus
Since
and we have
Taking standard parts, we are led to DEFINITION Let f be continuous on [a, b]. The average value of f between a and b is
Geometrically, the area under the curve y = f(x) is equal to the area under the constant curve y = fave between a and b,
|
|||
Home  Applications of the Integral Applications of the Integral  Averages Averages  Average Value Average Value |
|||
Last Update: 2006-11-25


 .
.
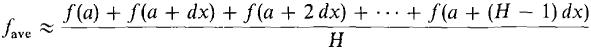
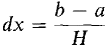 ,
,