Mass and Density - Two Dimenstions

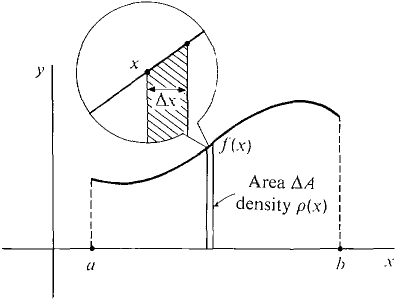
Imagine a flat plate which occupies the region below the curve y = f(x), f(x) ≥ 0, from x = a to x = b. If its density per unit area is a constant ρ gm/cm², then its mass is the product of the density and area,

Suppose instead that the density depends on the value of x, ρ(x). Consider a vertical strip of the plate of infinitesimal width Δx (Figure 6.6.3). On the strip between x and x + Δx, the density is everywhere infinitely close to ρ(x), so

Δm ≈ ρ(x) ΔA ≈ ρ(x) f(x) Δx       (compared to Δx).

Figure 6.6.3

By the Infinite Sum Theorem,

Example 2