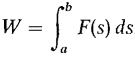Example 6

A semicircular plate of radius one, constant density, and mass m lies flat on the table,

(a) How much work is required to stand it up with the straight edge horizontal on the table (Figure 6.6.14(a))?

Figure 6.6.14 (a)

(b) How much work is required to stand it up with the straight edge vertical and one corner on the table (Figure 6.6.14(b))?

Figure 6.6.14 (b)

From the previous exercise, we know that the center of mass is on the central radius 4/3π from the center of the circle. Put the x-axis on the surface of the table.

(a)  The center of mass is lifted a distance 4/3π above the table. Therefore W = mg · 4/(3π).

(b)  The center of mass is lifted a distance 1 above the table, so W = mg.

Suppose a force F(s) varies continuously with the position s and acts on an object to move it from s = a to s = b. The work is then the definite integral of the force with respect to s,

To justify this formula we consider an infinitesimal length Δs. On the interval from 5 to s + Δs the force is infinitely close to F(s), so the work ΔW done on this interval satisfies

ΔW ≈ F(s) Δs (compared to Δs).

By the Infinite Sum Theorem,