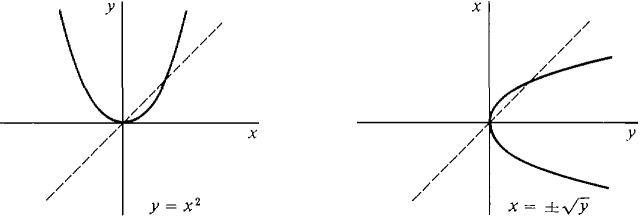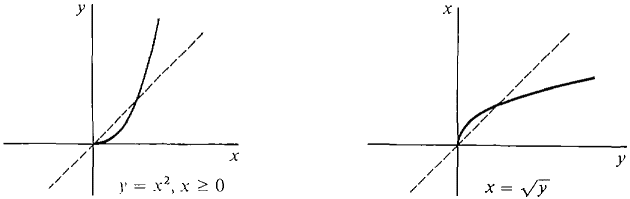Inverse Trigonometric Functions

Inverse functions were studied in Section 2.4. We now take up the topic again and apply it to trigonometric functions. A binary relation on the real numbers is any set of ordered pairs of real numbers. Thus a real function f of one variable is a binary relation such that for each x, either there is exactly one y with (a\ y) in f or there is no y with (x, y) in f. (Other important relations are x < y, x ≤ y, x ≠ y, x = y.)

The inverse of a function f may or may not be a function. For example, the inverse of y = x² is the relation x = ±√y, which is not a function (Figure 7.3.1). But the inverse of y = x², x ≥ 0, is the function x = √y (Figure 7.3.2).

Figure 7.3.1

Figure 7.3.2

Geometrically, the graph of the inverse relation of y = f(x) can be obtained by flipping the graph of y = f(x) about the diagonal line y = x (the dotted line in Figures 7.3.1 and 7.3.2). This flipping interchanges the x- and y-axes. This is because f(x) = y means (x, y) is in f, and g(y) = x means (y, x) is in g. It follows that:

If f and g are inverse functions then the range of f is the domain of g and vice versa.

Which functions have inverse functions? We can answer this question with a definition and a simple theorem.