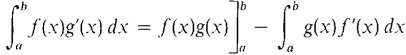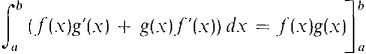Definite Integration By Parts

Integration by parts requires a great deal of guesswork. Given a problem ∫ h(x) dx we try to find a way to split h(x) dx into a product f(x) g'(x) dx where we can evaluate both of the integrals ∫ g'(x) dx and ∫ g(x) f'(x) dx.

Definite integrals take the following form when integration by parts is applied.

DEFINITE INTEGRATION BY PARTS

If u = f(x) and v = g(x) have continuous derivatives on an open interval I, then for a, b in I,

If we plot u = f(x) on one axis and v = g(x) on the other, we get a picture of definite integration by parts (Figure 7.4.1). The picture is easier to interpret if we change variables in the definite integrals and write the formula for integration by

Figure 7.4.1 Definite Integration by Parts parts in the form