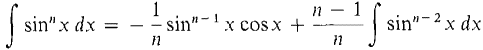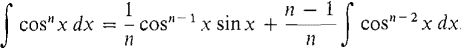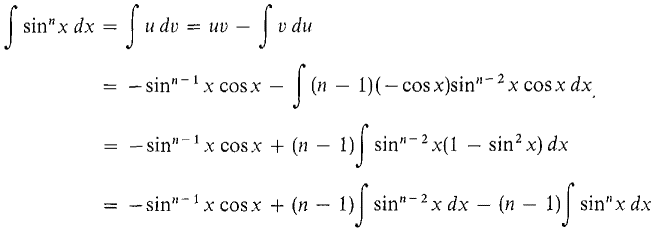Reduction Formulas (Sine and Cosine)

We will evaluate ∫ tan x dx in the next chapter.

Each time we use the reduction formula the exponent in the integral goes down by two. By repeated use of the reduction formulas we can integrate any even power of tan x or cot x. We can also work the integral of any odd power of tan x or cot x down to an expression involving ∫ tan x or ∫ cot x.

The reduction formulas for the other trigonometric functions are obtained by using integration by parts.

PROOF

(i) Break the term sinⁿ x dx into two parts,

sinⁿ x dx = sin^n-1 x(sin x dx).

We shall let 

u = sin^n-1 x, v = -cosx,

du = (n - 1)sin^n-2 x cosx dx, dv = sin x dx,

and use integration by parts. Then

We find that ∫ sinⁿ x dx appears on both sides of the equation, and we solve for it,

We already know the integrals

∫ sin x dx = -cos x + C,         ∫ cos x dx = sin x + C.

We can use the reduction formulas to integrate any positive power of sin x or cos x. Again, the formulas are true where n is any rational number, n ≠ 0.