| The ebook Elementary Calculus is based on material originally written by H.J. Keisler. For more information please read the copyright pages. |

|

Home  Trigonometric Functions Trigonometric Functions  Trigonometric Substitututions Trigonometric Substitututions  Examples Examples  Example 5: Trigonometric Substitution Example 5: Trigonometric Substitution |
|






|
|
Example 5: Trigonometric Substitution
The basic integrals: (a) (b) (c) can be evaluated very easily by a trigonometric substitution, (a)
Figure 7.6.6 Let θ = arcsin x (Figure 7.6.6). Then x = sin θ, dx = cos θ dθ,
(b)
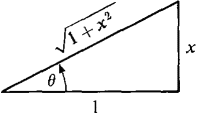
Figure 7.6.7 Let θ = arctan x (Figure 7.6.7). Then x = tan θ, dx = sec2 θ dθ,
(c)
Figure 7.6.8 Let θ = arcsec x (Figure 7.6.8). Then x = sec θ, dx = tan θ secθ dθ,
It is therefore more important to remember the method of trigonometric substitution than to remember the integration formulas (a), (b), (c).
|
|
Home  Trigonometric Functions Trigonometric Functions  Trigonometric Substitututions Trigonometric Substitututions  Examples Examples  Example 5: Trigonometric Substitution Example 5: Trigonometric Substitution |
|
Last Update: 2006-11-15


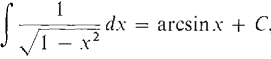

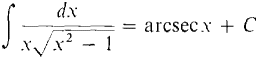 , x > 1
, x > 1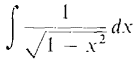

 = cos θ.
= cos θ.

 = sec θ.
= sec θ.
 , x > 1.
, x > 1.
 = tan θ.
= tan θ.