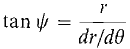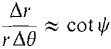The ebook Elementary Calculus is based on material originally written by H.J. Keisler. For more information please read the copyright pages.

Home Trigonometric Functions Slopes And Curve Sketching in Polar Coordinates Theorem 2: Direction of a Curve
 
del.icio.us Reddit Facebook StumbleUpon MySpace Twitter Search the VIAS Library  |  Index

Theorem 2: Direction of a Curve

The following theorem gives a simple formula for tan ψ when r ≠ 0.

THEOREM 2

Suppose r = f(θ) is a curve in polar coordinates and dr/dθ exists at a point P where r ≠ 0. Let L be the line tangent to the curve at P and let ψ be the angle between OP and L. Then

07_trigonometric_functions-462.gif

If dr/dθ ≠ 0,

07_trigonometric_functions-463.gif

07_trigonometric_functions-464.gif

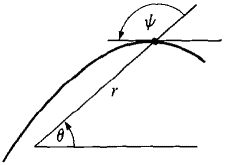
Figure 7.8.4

DISCUSSION

When r = Q, P is the origin so the line OP and angle ψ are undefined. The formula can be seen intuitively in Figure 7.8.4. Δθ is infinitesimal. As we move from the point P(r, θ) to the point Q(r + Δr, θ + Δθ) on the curve, the change in the direction perpendicular to OP will be very close to r Δθ, so we have

07_trigonometric_functions-465.gif07_trigonometric_functions-466.gif

We shall postpone the proof to the end of this section. We can use Theorem 2 in curve sketching as follows.

(a) In an interval where tan ψ > 0, the curve is going away from the origin as θ increases because dr/dθ has the same sign as r.

07_trigonometric_functions-467.gif

Figure 7.8.5(a)
(b) Where tan ψ < 0, the curve is going toward the origin as θ increases because dr/dθ has the opposite sign as c.

07_trigonometric_functions-468.gif

Figure 7.8.5(b)
(c)  Where r has either a local maximum or minimum and dr/dθ exists, the curve is going in a direction perpendicular to the radius. This is because dr/dθ = 0 so cot ψ = 0.

07_trigonometric_functions-469.gif

Figure 7.8.5(c)

Each of these cases is shown in Figure 7.8.5.
Home Trigonometric Functions Slopes And Curve Sketching in Polar Coordinates Theorem 2: Direction of a Curve

Last Update: 2006-11-05