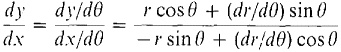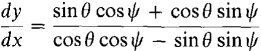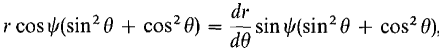The ebook Elementary Calculus is based on material originally written by H.J. Keisler. For more information please read the copyright pages.

Home Trigonometric Functions Slopes And Curve Sketching in Polar Coordinates Proof of Theorem 2
 
del.icio.us Reddit Facebook StumbleUpon MySpace Twitter Search the VIAS Library  |  Index

Proof of Theorem 2

PROOF OF THEOREM 2

Assume the curve is not vertical at the point P, that is, dx ≠ 0. Since x = r cos θ, y = r sin θ, we have

07_trigonometric_functions-480.gif

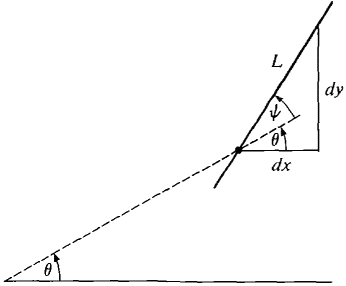
07_trigonometric_functions-481.gif

Figure 7.8.12

By the definition of the tangent line L (see Figure 7.8.12),

07_trigonometric_functions-482.gif

Using the addition formulas,

07_trigonometric_functions-483.gif

Thus

07_trigonometric_functions-484.gif

Multiplying out and canceling, we get

07_trigonometric_functions-485.gif

whence

07_trigonometric_functions-486.gif

If the curve is vertical at P we may use the same proof but with dx/dy instead of dy/dx.
Home Trigonometric Functions Slopes And Curve Sketching in Polar Coordinates Proof of Theorem 2

Last Update: 2006-11-05