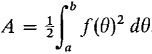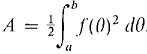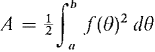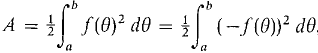| The ebook Elementary Calculus is based on material originally written by H.J. Keisler. For more information please read the copyright pages. |
|
Home  Trigonometric Functions Area in Polar Coordinates Theorem 2: Area of Region bounded by a Curve |
|
 Search the VIAS Library | Index
|
  |
Theorem 2: Area of Region bounded by a Curve
THEOREM 2 Let r = f(θ) be continuous and r ≥ 0 for a ≤ θ ≤ b, where b ≤ a + 2π. Then the region R bounded by the curve r = f(θ) and the lines 0 = a and 0 - b has area
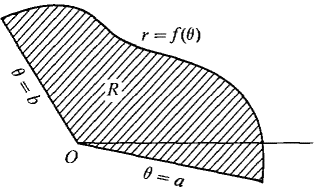
Discussion Imagine a point P moving along the curve r = f(θ) from θ = a to θ = b. The line OP will sweep out the region R in Figure 7.9.2. Since b ≤ a + 2π, the line will complete at most one revolution, so no point of R will be counted more than once.
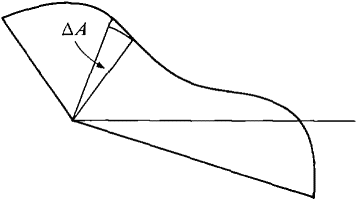
Figure 7.9.2 Figure 7.9.3 The formula for area can be seen intuitively by considering an infinitely small wedge ΔA of R between θ and θ + Δθ. (Figure 7.9.3). The wedge is almost a sector of a circle of radius j(θ) with central angle Δθ, so ΔA ≈ ½ f(θ)2 Aθ (compared to Δθ). By the Infinite Sum Theorem,
The actual proof follows this intuitive idea but the area of ΔA must be computed more carefully.
Figure 7.9.4 PROOF Let Δθ be positive infinitesimal and let θ be a hyperreal number between a and b - Aθ. Consider the wedge of R with area ΔA between θ and θ + Aθ. Since f(θ) is continuous, it has a minimum value m and maximum value M between θ and θ + Aθ, and furthermore, m ≈ f(θ), M ≈ f(θ). The sector between θ and Aθ of radius m is inscribed in ΔA while the sector of radius M is circumscribed about ΔA. (Figure 7.9.4 shows the inscribed and circumscribed sectors for real Aθ and infinitesimal Δθ.) By Theorem 1, the two sectors have areas ½m2 Δθ and ½M2 Δθ. Moreover, ΔA is between those two areas, ½m2 Δθ ≤ ΔA ≤ ½M2 Δθ, ½W ≤ ΔA/Aθ ≤ ½M2 Taking standard parts, ½f (θ)2 ≤ st(ΔA/Δθ) ≤ ½f (θ)2. Therefore ΔA/Aθ x ½f(θ)2, and by the Infinite Sum Theorem,
Theorem 1 is also true in the case that r = f(θ) is continuous and r ≤ 0. Since
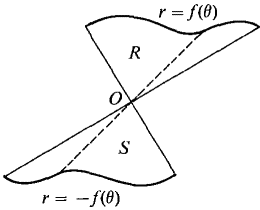
the region R bounded by the curve r = f(θ) has the same area as the region S bounded by the curve r = -f(θ). Both areas are positive. As we can see from Figure 7.9.5, S looks exactly like R but is on the opposite side of the origin.
Figure 7.9.5 Example 1: Area of a "Four-leaf Clover"Our next example shows why the hypothesis that r has the same sign for a ≤ θ ≤ b is needed in Theorem 2r.
|
|
| Home Trigonometric Functions Area in Polar Coordinates Theorem 2: Area of Region bounded by a Curve |
|
Last Update: 2006-11-08