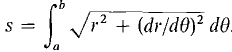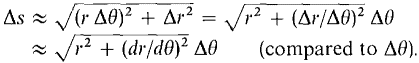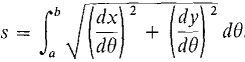| The ebook Elementary Calculus is based on material originally written by H.J. Keisler. For more information please read the copyright pages. |
|
Home  Trigonometric Functions Length of a Curve in Polar Coordinates Length of a Smooth Curve in Polar Coordinates |
|||||
 Search the VIAS Library | Index
|
  |
||||
Length of a Smooth Curve in Polar Coordinates
Consider a curve r = f(θ), a ≤ θ ≤ b in polar coordinates. The curve is called smooth if f'(θ) is continuous for θ between a and b. In Chapter 6 we obtained a formula for the length of a smooth parametric curve in rectangular coordinates. We may now apply this to get a formula for the length of a smooth curve in polar coordinates. THEOREM The length of a smooth curve r = f(θ), a ≤θ ≤b in polar coordinates which does not retrace itself is
or equivalently
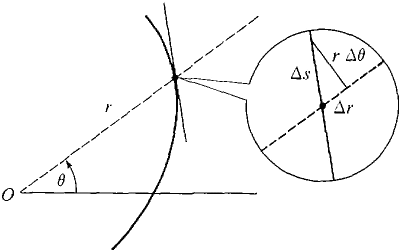
Discussion The formula can be seen intuitively as follows. We see from Figure 7.10.1 that
By the Infinite Sum Theorem,
Figure 7.10.1 The length of a curve has already been defined using rectangular coordinates, and the theorem states that the new formula will give the same number for the length. PROOF The curve is given in rectangular coordinates by the parametric equation x = f(θ) cos θ, y = f(θ) sin θ. The derivatives are
Since f(θ) and f'(θ) are continuous, dx/dθ and dy/dθ are continuous. Recall the length formula for parametric equations:
We compute
The desired formula now follows by substitution.
Example 2 proves that the length of an arc of the circle is equal to the angle formed by the ends of the arc and the origin. Note that if we take a = 0 and ft = 2π we get an arc length of 2π, which is twice the circumference of the circle. This is because the point (r, θ) goes around the circle twice, once from θ = 0 to θ = π and once from θ = π to θ = 2π.
|
|||||
| Home Trigonometric Functions Length of a Curve in Polar Coordinates Length of a Smooth Curve in Polar Coordinates |
|
||||
Last Update: 2006-11-25