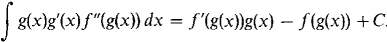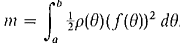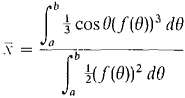| The ebook Elementary Calculus is based on material originally written by H.J. Keisler. For more information please read the copyright pages. |

|

Home  Trigonometric Functions Trigonometric Functions  Extra Problems for Chapter 7 Extra Problems for Chapter 7 |
|






|
|
Extra Problems for Chapter 7
11 An airplane travels in a straight line at 600 mph at an altitude of 4 miles. Find the rate of change of the angle of elevation one minute after the airplane passes directly over an observer on the ground. 12 A 40 ft ladder is to be propped up against a 15 ft wall as shown in the figure. What angle should the ladder make with the ground if the horizontal distance the ladder extends beyond the wall is to be a maximum?
24 Find the volume of the solid formed by rotating the region under the curve 25 Find the volume of the solid generated by rotating the region under the curve y = tan x, 0 ≤ x ≤ π/4, about the x-axis.
In Problems 31-34, sketch the given function in (a) rectangular coordinates, (b) polar coordinates. Let 0 ≤ θ ≤ 2π.
35 Find the area of the polar region bounded by r = 1 + sin2 θ. 36 Find the area of the polar region bounded by r - sin θ + cos θ. 37 Find the area of the polar region inside both the curves r = 1 - cos θ and r = 1 + cos θ. 38 Find the length in polar coordinates of the curve r = sin4(¼θ), 0 ≤ θ ≤ π. 39 Find the surface area generated by rotating the polar curve r = 1 - cos θ, 0 ≤ θ ≤ 7π/2, about the x-axis. 40 Use the Intermediate Value Theorem to prove that arctan y has domain (- ∞, ∞). 41 Use the Intermediate Value Theorem to prove that the domain of arcsec y is the set of all y such that y ≤ - 1 or y ≥ 1. 42 Prove that if/ is a differentiable function of x then
43 If u and v are differentiable functions of x then
44 Show that if f' and g are differentiable for all x then
45 Use integration by parts to prove the reduction formula
Hint: 46 Suppose y = f(x), a < x < b and x = g(y), c < y < d are inverse functions and are strictly increasing. Let y0 = f(x0). Prove that: (a) If f is continuous at x0, g is continuous at y0. (b) If f' (x0) exists and f'(x0) ≠ 0, then g'(y0) exists. 47 Justify the following formula for the area of the polar region bounded by the continuous curves θ = f(r), θ = g(r), a ≤ r ≤b, where 0 ≤ f(r) ≤ g(r) ≤ 2π.
48 Justify the following formula for the mass of an object in the polar region 0 ≤ r ≤ f(θ), a ≤ θ ≤b, with density ρ(θ) per unit area.
49 Justify the following formulas for the centroid of the polar region 0 ≤ r ≤ f(θ), a ≤ θ ≤ b.
Hint: The centroid of a triangle is located on a median ⅔ of the way from a vertex to the opposite side. 50 Find the centroid of the sector 0 ≤ r ≤ c, a ≤ θ ≤ b. 51 Find the centroid of the region bounded by the cardioid r = 1 + cos θ.
|
|
Home  Trigonometric Functions Trigonometric Functions  Extra Problems for Chapter 7 Extra Problems for Chapter 7 |
|
Last Update: 2006-11-25


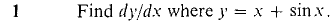


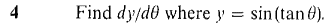


















 0 ≤ x ≤ π, about the x-axis.
0 ≤ x ≤ π, about the x-axis.