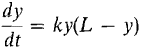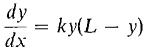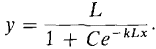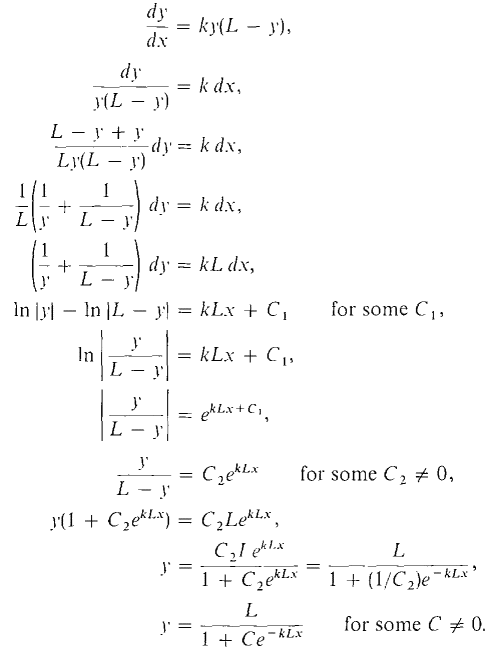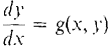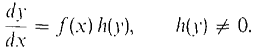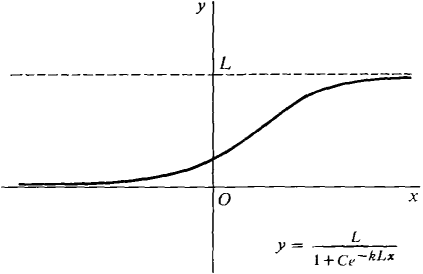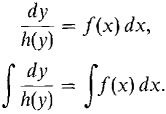Theorem 2: General Solution Differential Equation

As we mentioned at the beginning of this chapter, the exponential growth function y = Ce^kt is unrealistic for populations except for short periods of time. Here is a more realistic, but still quite simple, population growth function.

A population often has a limiting value L at which overcrowding will overcome reproduction. It is reasonable to suppose that the growth rate dy/dt is proportional to both the population y and the difference L - y. That is, the population satisfies the differential equation

for some constant k. The spread of an epidemic also satisfies this differential equation, where y is the number of victims and L is the total population. That is, the rate of increase of the number of victims is proportional to the product of the number of victims and the remaining population.

The important case of this function is where C, k, and L are positive constants. In this case the function is called a logistic function. As the graph in Figure 8.6.1 shows, the value of the function approaches zero as t → - x and L as r → x ; that is,

lim_x→∞ y = 0, lim_x→-∞ y = L.

A population given by this function will approach but never quite reach the limiting value L.

It is easy to see intuitively that a differential equation

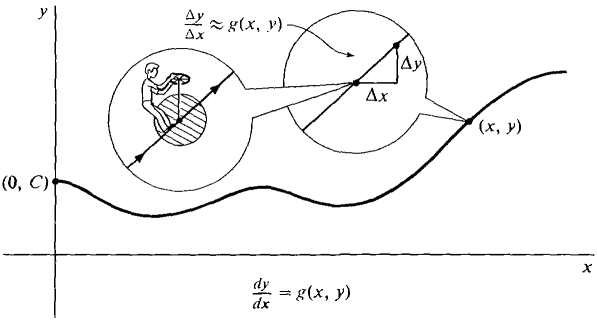
will have a solution if the function g(x, y) behaves reasonably. We return to our picture of a moving point controlled by a little man with a steering wheel (Figure 8.6.2). At x = 0 the point starts at y = C. (This is the initial condition.) At each value of x, the little man computes the value of g(x, y) and turns the steering wheel so that the slope will be dy/dx = g(x, y). Then the curve traced out by the point will be a solution of the differential equation. In general, there will always be a family of solutions which depend on the constant C of the initial condition.

Using indefinite integrals we can solve any differential equation where dy/dx is equal to a product of a function of x and a function of y,

(4)

Figure 8.6.1

Figure 8.6.2

We simply separate the x and y terms and integrate,

In an equation of the form (Equation 4) the variables are said to be separable.