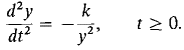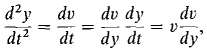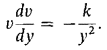| The ebook Elementary Calculus is based on material originally written by H.J. Keisler. For more information please read the copyright pages. |

|

Home  Exponential and Logartihmic Functions Exponential and Logartihmic Functions  Extra Problems for Chapter 8 Extra Problems for Chapter 8 |
|






|
|
Extra Problems for Chapter 8
24 A falling object of mass m is subject to a force due to gravity of - mg and a force due to air resistance of -kv, where v is its velocity. If v = 0 at time t = 0, find v as a function of time. 25 The pressure P and volume V of a gas in an adiabatic process (a process with no heat transfer) are related by the differential equation
where k is constant. Solve for P as a function of V. 26 An electrical condenser discharges at a rate proportional to its charge Q, so that dQ/dt = -kQ for some constant k. If the charge at time t = 0 is Q0, find Q as a function of t. 27 Newton's Law of Cooling states that a hot object cools down at a rate proportional to the difference between the temperature of the object and the air temperature. If the object has temperature 140° an = 0, 100° at t = 10, and 80° at t = 20, find the temperature y of the object as a function of f, and find the air temperature.
35 Find the surface area generated by rotating the curve y - sin x, 0 ≤ x ≤ π, about the x-axis. 36 Find the surface area generated by rotating the parabola y = x2, 0 ≤ x ≤ 1, about the y-axis. 37 Approximate e0.03 and give an error estimate. 38 Approximate ln (0.996) and give an error estimate. 39 Use the trapezoidal rule with Δx = 1 to approximate In 6 and give an error estimate. 40 Find the centroid of the region under the curve y = ex, 0 ≤ x ≤ 1. 41 Find the centroid of the region under the curve y = ln x, 1 ≤ x ≤ 2. 42 Find the length of the curve y = ex, 0 ≤ x ≤ 1. 43 Find the surface area generated by rotating the curve y = ex, 0 ≤ x ≤ 1, about the x-axis. 44 Obtain a reduction formula for ∫ xnex dx. 45 Prove that the function y = xx, x > 0, is continuous, using the continuity of ln x and ex 46 Let y = f(x) be a function which is continuous on the whole real line and such that for all u and v, f(u + v) = f(u)f(v). Prove that f(x) = ax where a = f(1). Hint: First prove it for x rational. 47 Prove that for all x > 0,
Hint: Use the formula
48 Prove that the function f(x) = (1 + 1/x)x is increasing for x > 0. 49 Show that the improper integral 50 Show that 51 The inverse square law for gravity shows that an object projected vertically from the earth's surface will rise according to the differential equation (1)
Here y is the height above the earth's center. If v = dy/dt is the velocity at time t, then
so Equation 1 may be written as (2)
Assume that at time t = 0, y = 4000 miles (the radius of the earth) and v = v0 (the initial velocity). Solve for velocity as a function of y. Find the escape velocity, i.e., the smallest initial velocity v0 such that the velocity v never drops to zero.
|
|
Home  Exponential and Logartihmic Functions Exponential and Logartihmic Functions  Extra Problems for Chapter 8 Extra Problems for Chapter 8 |
|
Last Update: 2010-11-25


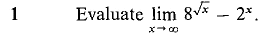
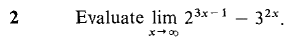
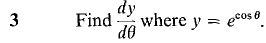
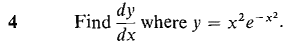
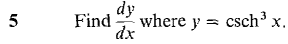

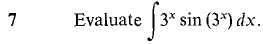
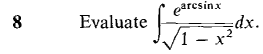
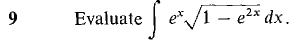
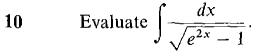



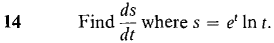
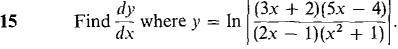
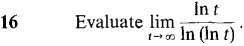

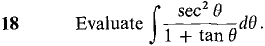
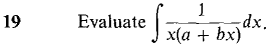



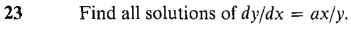
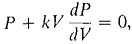
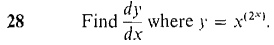
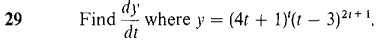
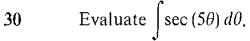
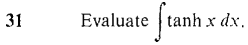


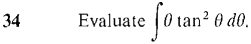
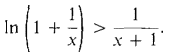
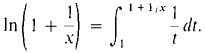
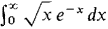 converges. Hint: Show that the definite integrals
converges. Hint: Show that the definite integrals 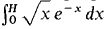 are finite and have the same standard part for all positive infinite H.
are finite and have the same standard part for all positive infinite H.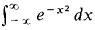 converges.
converges.