| The ebook Elementary Calculus is based on material originally written by H.J. Keisler. For more information please read the copyright pages. |

|

Home  Infinite Series Infinite Series  Sequences Sequences  Theorem 1: Sequences approaching ∞ Theorem 1: Sequences approaching ∞ |
|||






|
|||
Theorem 1: Sequences approaching ∞
THEOREM 1 Each of the following sequences approaches ∞. limn→∞ n! = ∞, limn→∞ bn = ∞ if b > 1, limn→∞ nc = ∞ if c > 0, limn→∞ ln(n) = ∞. Moreover, each sequence in the list grows faster than the next one, (i) (ii) (iii) PROOF Let H be positive infinite. We already know that ln H is positive infinite. We must show that each of the following are also positive infinite.
It is easier to show that their logarithms are positive infinite. We need the fact that, by l'Hospital's rule for ∞/∞,
so (i)
> (H - m) ln m - H ln b = H(ln m - ln b) - m ln m. Since m > b. ln m > ln b, and ln (H!/bH) is positive infinite. (ii)
Since b > 1, ln b > 0. (ln H)/H is infinitesimal. Therefore ln(bH/Hc) is positive infinite, (iii)
Since c > 0, K is infinite, and (ln K)/K is infinitesimal, ln(Hc/ln H)) is positive infinite. Note: For n = 1, the term nc/(ln n) is undefined, so we should start the sequence with n = 2.
COROLLARY (i) limn→∞ b-n = 0 if b > 1. (ii) limn→∞ n-c = 0 if c > 0.
|
|||
Home  Infinite Series Infinite Series  Sequences Sequences  Theorem 1: Sequences approaching ∞ Theorem 1: Sequences approaching ∞ |
|||
Last Update: 2006-11-07


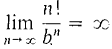 (b > 1),
(b > 1), (b > 1, c> 0),
(b > 1, c> 0),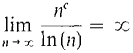 (c > 0).
(c > 0).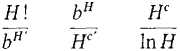

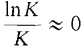 for all infinite K.
for all infinite K. . Let m > b. Then
. Let m > b. Then = ln 1 + ... + ln (m - 1) + ln m + ... + ln H - H ln b
= ln 1 + ... + ln (m - 1) + ln m + ... + ln H - H ln b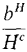

 . Let K = ln H.
. Let K = ln H.
