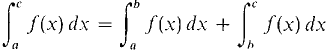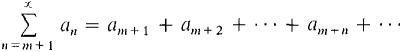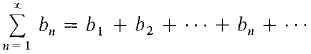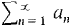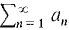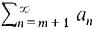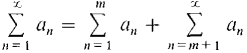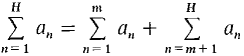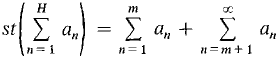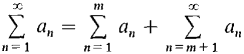| The ebook Elementary Calculus is based on material originally written by H.J. Keisler. For more information please read the copyright pages. |
|
Home  Infinite Series Properties of Infinite Series Theorem 2: Tail Of a Series |
|||
 Search the VIAS Library | Index
|
  |
||
Theorem 2: Tail Of a Series
The next theorem corresponds to the Addition Property for integrals,
DEFINITION The series
is defined as
where bn = am+n. This series is called a tail of the original series THEOREM 2 A series
converges if and only if its tail converges for any m. The sum of a convergent series is equal to the mth partial sum plus the remaining tail,
or a1 + ... + an + ... = (a1 + ... + am) + (am+1 + ... + am+n + ...). PROOF First assume the tail converges. For any infinite H, we have a1 + ... + aH = (a1 + ... + am) + (am+1 + ... + aH), or Taking standard parts,
Therefore the series converges and
If we assume the series converges we can prove the tail converges in a similar way.
|
|||
| Home Infinite Series Properties of Infinite Series Theorem 2: Tail Of a Series |
|
||
Last Update: 2006-11-07