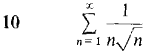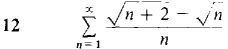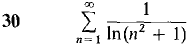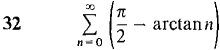| The ebook Elementary Calculus is based on material originally written by H.J. Keisler. For more information please read the copyright pages. |

|

Home  Infinite Series Infinite Series  Series With Positive Terms Series With Positive Terms  Problems Problems |
|






|
|
Problems
Test the following series for convergence.
Use the Integral Test to determine whether the following improper integrals converge or diverge.
41 Prove that if each an is positive and Y^= i an converges, then £n'= t <*l converges. 42 Using Theorem 1 (page 539), prove that a negative term series either converges or diverges to -∞.
|
|
Home  Infinite Series Infinite Series  Series With Positive Terms Series With Positive Terms  Problems Problems |
|
Last Update: 2006-11-25