Elementary Calculus: Alternating Series Test

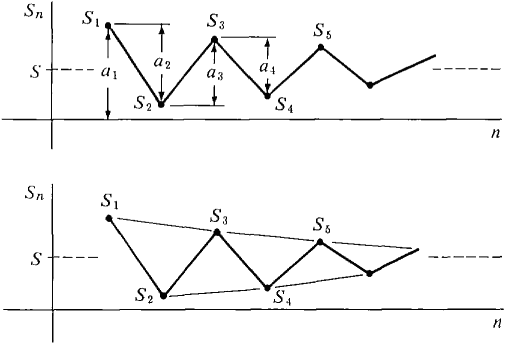
We see from the graph in Figure 9.5.1 that the partial sums S_n alternately increase and decrease, but the change is less each time. The value of S_n"vibrates" back and forth and the vibration damps down around the limit S.

PROOF

The sequence of even partial sums is increasing.

S₂ < 5₄ < ... < S_2n < ...,

because

S₄ = S₂ + (a₃ - a₄), S₆ = S₄ + (a₅ - a₆), etc.

The sequence of odd partial sums is decreasing,

S₁ > S₃ > S₅ > ...,

for

S₃ = S₁ - (a₂ - a₃), S₅ = S₃ - (a₄ - a₅), etc.

Figure 9.5.1

It follows that each even partial sum is less than S_x,

S₁ > S₁ - a₂ = S₂, S₁ > S₃ - a₄ = S₄, S₁ > S₅ - a₆ = S₆, etc.

Theorem 1 (Section 9.4) shows that the increasing sequence of even partial sums converges,

lim_n→∞ S_2n = S.

Given any infinite H, a_2H+l ≈ 0 and S_2H ≈ S, so

S_2H+1 = S_2H + a_2H+1 ≈ S

Therefore the sequence of all partial sums converges to S, and

Finally, since the even partial sums are increasing and the odd partial sums are decreasing, we have the estimate

S_2n < S < S_2n+1.

The Cauchy Test for Divergence in Section 9.2 shows that if the terms an do not converge to zero the series diverges.

We have now built up quite a long list of convergence tests. The next section contains one more important test, the Ratio Test. At the end of that section is a summary of all the convergence tests with hints on when to use them.