| The ebook Elementary Calculus is based on material originally written by H.J. Keisler. For more information please read the copyright pages. |

|

Home  Infinite Series Infinite Series  Absolute and Conditional Convergence Absolute and Conditional Convergence  Theorem 1: Convergence of Absolutly Convergent Series Theorem 1: Convergence of Absolutly Convergent Series |
|||||






|
|||||
Theorem 1: Convergence of Absolutly Convergent Series
THEOREM 1 Every absolutely convergent series is convergent. That is, if the absolute value series Discussion This theorem shows that if a positive term series then it remains convergent if we make some or all of the terms bn negative, because the new series will still be absolutely convergent. Given an arbitrary series following three things can happen: The series is absolutely convergent. The series is conditionally convergent. The series is divergent. PROOF OF THEOREM 1 We use the Sum Rule. Assume let bn = an + |an|. Then an = bn - |an| and
(See Figure 9.6.1).
Figure 9.6.1 Both Moreover,
converges. Then using the Sum and Constant Rules,
converges.
|
|||||
Home  Infinite Series Infinite Series  Absolute and Conditional Convergence Absolute and Conditional Convergence  Theorem 1: Convergence of Absolutly Convergent Series Theorem 1: Convergence of Absolutly Convergent Series |
|||||
Last Update: 2006-11-07


 converges, then
converges, then  converges.
converges. is convergent,
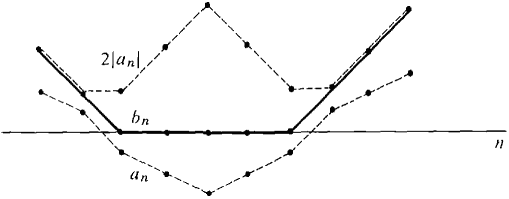
is convergent,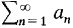 , the theorem shows that exactly one of the
, the theorem shows that exactly one of the converges and
converges and
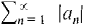 and
and 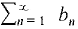 have nonnegative terms.
have nonnegative terms. converges and bn ≤ 2 |an|. By the Comparison Test,
converges and bn ≤ 2 |an|. By the Comparison Test,

