| The ebook Elementary Calculus is based on material originally written by H.J. Keisler. For more information please read the copyright pages. |

|

Home  Infinite Series Infinite Series  Absolute and Conditional Convergence Absolute and Conditional Convergence  Comparison Tests for Absolute Convergence Comparison Tests for Absolute Convergence |
|||||||






|
|||||||
Comparison Tests for Absolute Convergence
The comparison tests for positive term series give us tests for absolute convergence. COMPARISON TEST
LIMIT COMPARISON TEST
RATIO TEST
PROOF (i) Choose b with L < b < 1. By the ε, N condition, there is an N such that all the ratios
are less than b. Therefore with c = |aN|. |aN+l| < cb, |aN + 2| < cb2,...,|aN + n| < cb",.... The geometric series (ii) By the ε, N condition there is an N such that the ratios
are all greater than one. Therefore |aN| < |aN+1| < ... < |aN+n| < .... It follows that the terms an do not converge to zero, so the series The Ratio Test is useful even for positive term series, and is often effective for series involving n! and an.
|
|||||||
Home  Infinite Series Infinite Series  Absolute and Conditional Convergence Absolute and Conditional Convergence  Comparison Tests for Absolute Convergence Comparison Tests for Absolute Convergence |
|||||||
Last Update: 2006-11-07


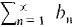 is absolutely convergent then
is absolutely convergent then  is absolutely convergent.
is absolutely convergent. is absolutely convergent then
is absolutely convergent then  is absolutely convergent.
is absolutely convergent.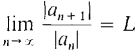
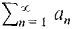 converges absolutely.
converges absolutely.
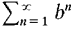 converges, so by the Comparison Test, the tail
converges, so by the Comparison Test, the tail  converges. Therefore the absolute value series
converges. Therefore the absolute value series 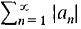 converges.
converges.
 diverges.
diverges.