| The ebook Elementary Calculus is based on material originally written by H.J. Keisler. For more information please read the copyright pages. |
|
Home  Infinite Series Power series Corollary: Interval of Convergence |
|||||||||||
 Search the VIAS Library | Index
|
  |
||||||||||
Corollary: Interval of Convergence
COROLLARY For each power series (i) The series converges absolutely at x = 0 and diverges everywhere else. (ii) The series converges absolutely on the whole real line (-∞, ∞). (iii) The series converges absolutely at every point in an open interval (-r, r) and diverges at every point outside the closed interval [-r, r]. At the endpoints -r and r the series may converge or diverge, so the interval of convergence is one of the sets (-r,r), [-r, r), (-r, r], [-r, r]. Figure 9.7.1 illustrates part (iii) of the Corollary. The number r is called the radius of convergence of the power series. In case (i) the radius of convergence is zero, and in case (ii) it is ∞. Once the radius of convergence is determined, we need only test the series at x = r and x = -r to find the interval of convergence.
Figure 9.7.1
If we replace x by x - c we obtain a power series in x - c,
The power series and the interval of convergence is simply moved over so that its center is c instead of 0. For example, if
has interval of convergence (c - r, c + r], illustrated in Figure 9.7.2.
Figure 9.7.2
|
|||||||||||
| Home Infinite Series Power series Corollary: Interval of Convergence |
|
||||||||||
, one of the following happens.
has the same radius of convergence as 
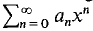has interval of convergence (- r, r], then
Last Update: 2006-11-08