| The ebook Elementary Calculus is based on material originally written by H.J. Keisler. For more information please read the copyright pages. |

|

Home  Infinite Series Infinite Series  Derivatives and Integrals of Power Series Derivatives and Integrals of Power Series  Power Series Formulas Power Series Formulas |
|






|
|
Power Series Formulas
We shall now get several new power series formulas starting from the power series for 1/(1 - x). We shall use the following methods:
Methods C, D, and G may change the radius of convergence. We start with (1)
Substitute -u for x in Equation 1. (2)
The radius of convergence is still r = 1 because when |- u| < 1, |u| < 1. Let us instead substitute 2u for x in Equation 1 and see what happens to the radius of convergence. (3)
The radius of convergence in Equation 3 is r = ½ because when |2u| < 1, |u| < ½. For convenience we rewrite Equations 2 and 3 with x's instead of u's. Thus (2)
By integrating 1/(1 - x) and multiplying by - 1 we get a power series for ln (1 - x).
(4) We next use the power series Equation 2 for 1/(1 + x). Substitute x2 for x in Equation 2. (5)
r is still 1 because if |x2| < 1, |x| < 1. We obtain a power series for arctan x by integrating (5).
(6)
Finally let us differentiate the series (1) for 1/(1 - x).
(7) Let us begin again, this time with (8) Substitute -x for x in Equation 8. (9) Using the formulas
we can obtain power series for cosh x and sinh x. This is our first chance to use the method of adding power series. (10) (11) Notice that the odd terms cancel out for cosh x and the even terms cancel out for sinh x. In Section 9.11 we shall obtain power series for sin x and cos x by another method. We can easily get new power series by multiplying by xp. For example, starting with the power series for ln (1 - x), we obtain
and so on. Since the series for ln (1 - x) has no constant term, we may also divide by x to get a new power series. To cover the case x = 0, we let
Then
We can often get a power series formula for an indefinite integral which cannot be evaluated in other ways. For example, the integral
is of central importance in probability theory. It is the area under the normal (bell-shaped) curve y - e-x². This integral is not an elementary function at all, so the methods of integration in Chapter 9 will fail. However, we can easily find a power series for this integral. First substitute x2 for x in Equation 9. (12) Then integrate. (13)
|
|
Home  Infinite Series Infinite Series  Derivatives and Integrals of Power Series Derivatives and Integrals of Power Series  Power Series Formulas Power Series Formulas |
|
Last Update: 2006-11-08


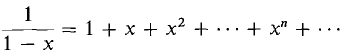 , r = 1.
, r = 1. 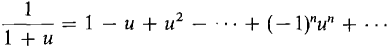 , r = 1.
, r = 1.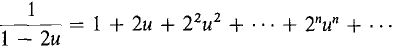 , r = ½.
, r = ½.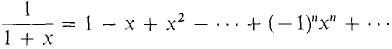 , r=1.
, r=1.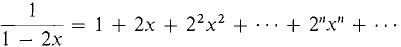

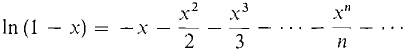 , r = 1.
, r = 1.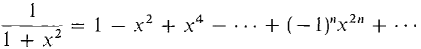 , r = 1.
, r = 1.
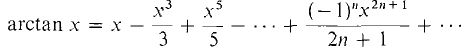 , r=1.
, r=1. 
 , r = 1.
, r = 1.  , r = ∞
, r = ∞ 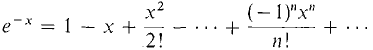 , r = ∞.
, r = ∞.  ,
, 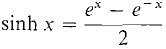
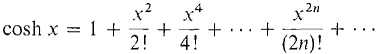 , r = x.
, r = x. , r = ∞.
, r = ∞.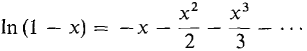 r = 1,
r = 1,  , r = 1,
, r = 1,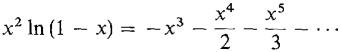 r = 1,
r = 1,
 , r = 1.
, r = 1.
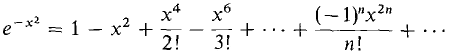 , r = ∞.
, r = ∞. , r = ∞.
, r = ∞.