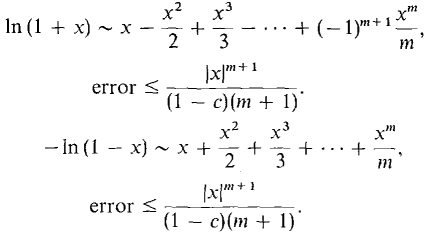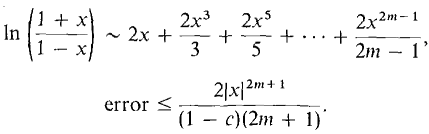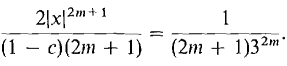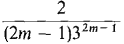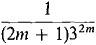| The ebook Elementary Calculus is based on material originally written by H.J. Keisler. For more information please read the copyright pages. |

|

Home  Infinite Series Infinite Series  Approximating Power Series Approximating Power Series  Examples Examples  Example 7 Example 7 |
|||||||||||||||||||||||||






|
|||||||||||||||||||||||||
Example 7
Find an error estimate for the power series for ln((1 + x)/(1 - x)) valid for - c ≤ x ≤ c. Use it to approximate ln 2 within 0.00001. From Example 5 we have the following error estimates for in (l + x) and - ln (1 - x) valid for - c ≤ x ≤ c.
We add the two sums and error estimates,
We wish to choose x so that (1 + x)/(l - x) = 2. Solving for x we get x = ⅓. Now set c = 5 and x = ⅓. The error estimate for x = ⅓ is
The error estimate drops below 0.00001 when m = 5. Thus ln 2 ~ 0.693146, error ≤ 0.00001.
|
|||||||||||||||||||||||||
Home  Infinite Series Infinite Series  Approximating Power Series Approximating Power Series  Examples Examples  Example 7 Example 7 |
|||||||||||||||||||||||||
Last Update: 2006-11-15