| The ebook Elementary Calculus is based on material originally written by H.J. Keisler. For more information please read the copyright pages. |

|

Home  Infinite Series Infinite Series  Approximating Power Series Approximating Power Series  Problems; Problems; |
|






|
|
Problems;
Problems 1-12 below are to be done using a power series with an error estimate. If a hand calculator is available they can be worked with the errors reduced by an additional factor of 1000. 1 Approximate ln (1.2) within 0.01. 2 Approximate arctan (1/10) within 10-7. 3 Approximate e-1/4 within 0.00001. 4 Approximate 5 Approximate 6 Approximate 7 Approximate 8 Approximate 9 Approximate 1/(1 - 0.003) within 0.0001. 10 Approximate ln 3 within 0.1 by the method of Example 6. Hint: ln 3 = -ln(1 - x) where x = ⅔. 11 Approximate ln 3 within 0.001 by the method of Example 7. 12 (a) Approximate ln (1½) within 0.00001 by the method of Example 7. (b) Approximate ln 3 within 0.00002 using the formula ln 3 = ln 2 + ln (½). In Problems 13-18 find a power series approximation with an error estimate for f(x) valid for -½ ≤ x ≤ ½. Then approximate f(½) within 0.01. 13 14 15 16 Hint: x2 = ¼ when x = ½. 17
19 Using the power series for arctan x at x = 1, show that
20 Using the power series for
|
|
Home  Infinite Series Infinite Series  Approximating Power Series Approximating Power Series  Problems; Problems; |
|
Last Update: 2006-11-25


 within 0.01.
within 0.01. within 0.0001.
within 0.0001.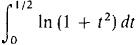 within 0.001.
within 0.001. within 0.0001.
within 0.0001. within 0.00001.
within 0.00001.

 .
.



 at x = 1, show that
at x = 1, show that