| The ebook Elementary Calculus is based on material originally written by H.J. Keisler. For more information please read the copyright pages. |

|

Home  Vectors Vectors  Vector Algebra Vector Algebra  Vectors Vectors |
|||||||||||||||||||||






|
|||||||||||||||||||||
Vectors
Usually we are not really interested in the exact placement of a directed line segment DEFINITION The family of all directed line segments with the same components as Since all directed line segments with the same components have the same length and direction, a vector may be regarded as a quantity which has length and direction. Vectors arise quite naturally in both physics and economics. Here are some examples of vector quantities.
We shall now begin the algebra of vectors. In vector algebra, real numbers are called scalars. We study two different kinds of quantities, scalars and vectors. The length (or norm) of a vector A is the distance between P and Q where
The length of a position vector is the distance from the origin. The length of a
Figure 10.1.5 Length of a Vector velocity vector is the speed of a particle. The length of a force vector is the magnitude of the force. The length of a displacement vector is the distance moved. For price or commodity vectors, the notion of length does not arise in a natural way.
The vector with components (0, 0) is called the zero vector, denoted by 0. The zero vector is represented by the degenerate line segments
|
|||||||||||||||||||||
Home  Vectors Vectors  Vector Algebra Vector Algebra  Vectors Vectors |
|||||||||||||||||||||
Last Update: 2006-11-07


 on the (x, y) plane, but in the length and direction of
on the (x, y) plane, but in the length and direction of  . These can be determined by the x and y components of
. These can be determined by the x and y components of  . We are thus led to the notion of a vector.
. We are thus led to the notion of a vector. will be called the
will be called the 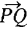 represents this vector.
represents this vector.
 represents A. The length is a scalar, denoted by |
represents A. The length is a scalar, denoted by |

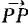 . It has no direction. The length of the zero vector is zero, while the length of every other vector is a positive scalar.
. It has no direction. The length of the zero vector is zero, while the length of every other vector is a positive scalar.